Weaire-Phelan Structure

by Tuğrul Yazar | May 15, 2013 01:27

Becoming popular after the Beijing 2008 Olympics National Aquatics Centre[1]‘s facade (which is believed to be a Voronoi[2] subdivision, as an epic mistake), the Weaire Phelan structure is a solution of equal volumes with minimal surface area. Although it is a structural solution, I think for architects, catching the eye with “cute bubbles” seems to be the primary purpose of this structure.

(images from arup.com)

A More Formal Explanation

This nice website [3]briefly explains the phenomenon, along with a paper model of it;

Lord Kelvin posed the question of how space could be divided into cells of equal volume and minimal surface area. This is equivalent to asking what shape equal-sized soap bubbles would take in foam since bubbles naturally assume shapes with minimal surface area. He conjectured that the solution was a lattice of truncated octahedra with slightly curved hexagonal faces. The polyhedral version of this structure is called the Kelvin structure. The physicists Denis Weaire and Robert Phelan applied a structure known from crystallography to the problem and found that the so-called Weaire Phelan structure improves on the Kelvin structure.

There[4] is also a great implementation on Grasshopper / Rhino by Jon Mirtschin. It is now a ready-made component in Grasshopper[5] and also a plug-in for Rhino[6]. But I’m not much into quick visual outputs nowadays. Instead, I wonder how Mr. Mirtschin’s mind solved that question in coding. I believe this is more important for me. This blog page[7] covers a good explanation with a nice poster, showing the slicing for the National Aquatics Centre design. There are also countless more efforts to draw this structure in Grasshopper and Rhinoscript. It somehow became a cult exercise for those interested in contemporary architectural geometry nowadays. Below is the sequence of my research and modeling process;

You can easily draw both components (irregular dodecahedron and Tetrakaidecahedron[8]) by using vertex coordinates. It seemed at first, that there is no other way to draw these shapes. Here, the Tetrakaidecahedron is generally confused with, but not a regular Truncated Octahedron, named Kelvin’s Tetrakaidecahedron.

Modeling Steps of Weaire Phelan Structure

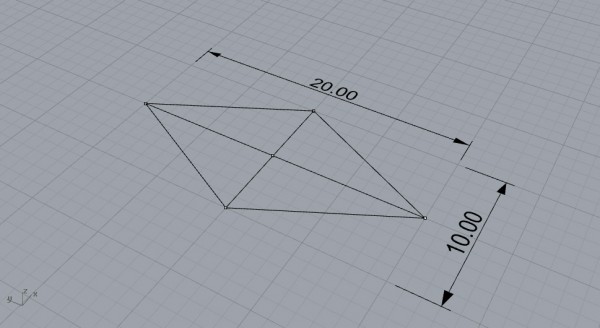
First, you need to define the overall size of the polyhedron[9]. Here, I’ll use 20×10 for the initial rhombus so that we’ll be able to check with the vertex coordinates given on the above website. Thus, we start with a rhombus with a 2/1 ratio in diagonals.

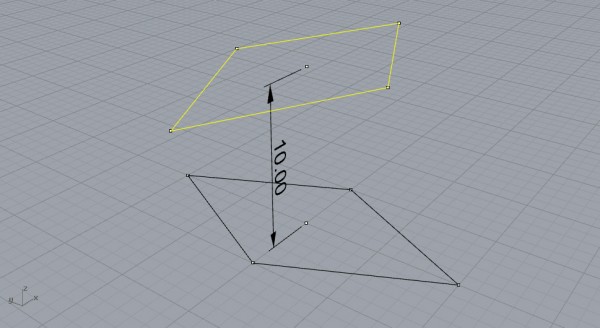
Now, copy the rhombus by 10 (smaller of the diagonals) and rotate 90 degrees.

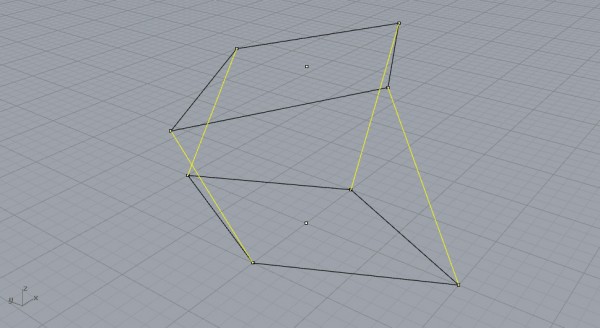
Connect the vertices of the two rhombi as shown above.

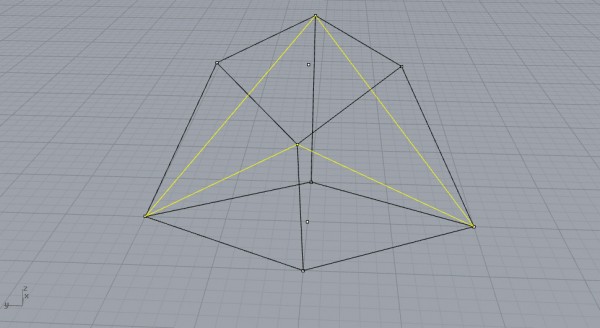
Also, connect the vertices sideways to create equal triangles. Now, put triangle and quad planar faces to create a 10-sided irregular polyhedron, as shown below:

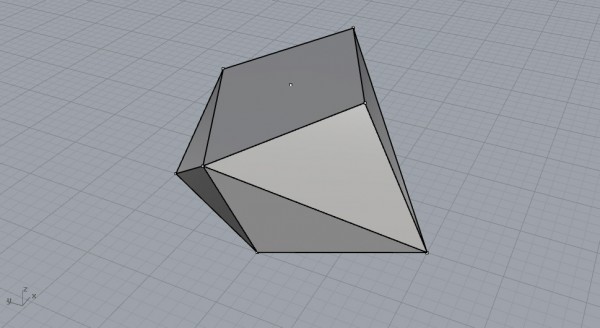
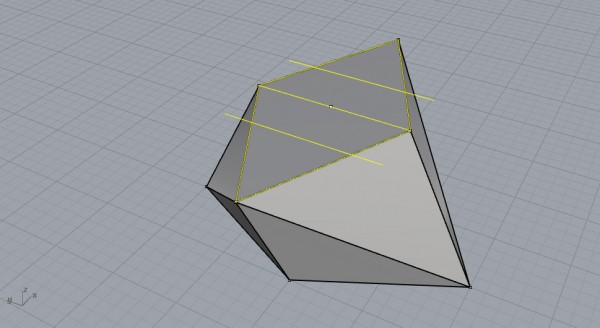
Continue by drawing the short diagonal of the rhombi and copy it to 3.7 units (for 10) in both directions. Yes, it’s cheating a geometric construction to use numeric measurements. But I couldn’t find a better way to find this edge distance. Also, it is interesting to think how this 3.7 would work, really. I think this is another interesting question for the future.

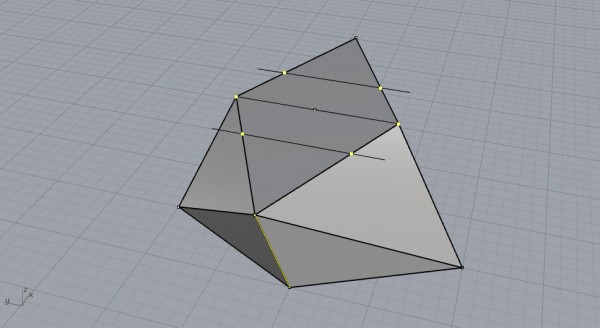
These intersections will create the irregular hexagon of the polyhedron. We’ll have to transfer the edge lengths at the far corners of the rhombi;

Cutting with Spheres

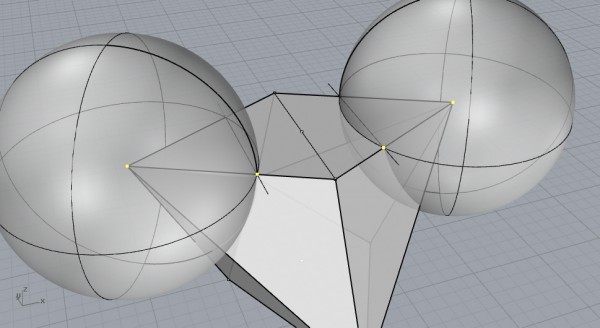
Put two spheres centered at far vertices of the rhombi, by pointing to the new (3.7) intersections to define radii. You will transfer these radii like this;

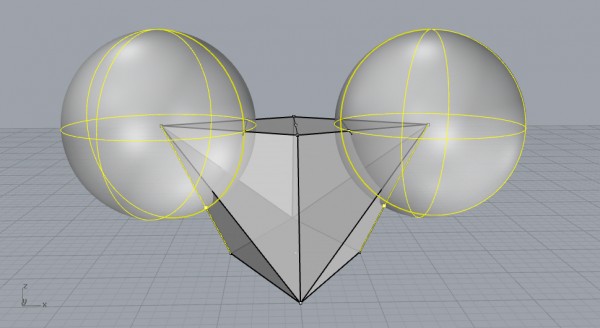
Select the edges shown above and intersect the spheres to get those two points. Just hide the spheres and you’ll see these three points;

You will use these three points to define cutting planes while trimming the 10-sided polyhedron. But now, you’ll have to repeat the above steps for the second rhombus as shown below.

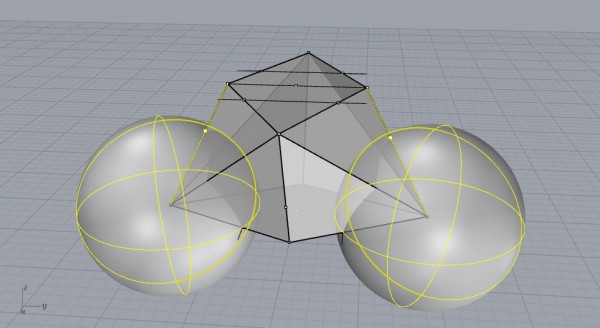
Be careful that you rotated the second rhombus by 90 degrees. So you’ll put spheres in opposite directions and get the intersection points. Finally, you’ll get something like this;

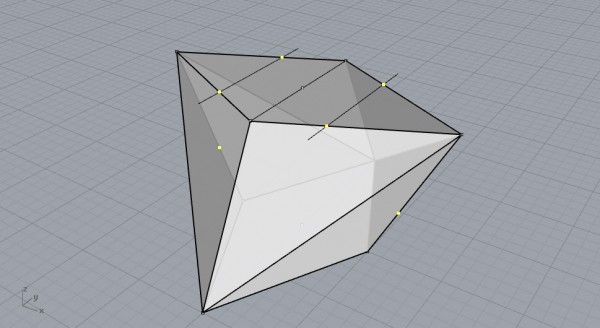
Now, cut the polyhedron using those points in a fashion. So, this will trim all four sharp corners of the rhombii.

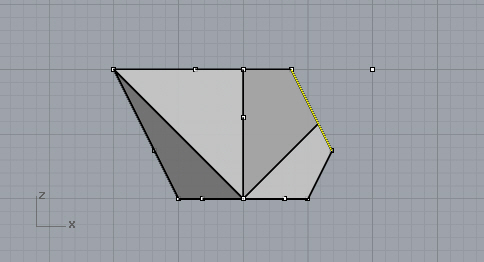
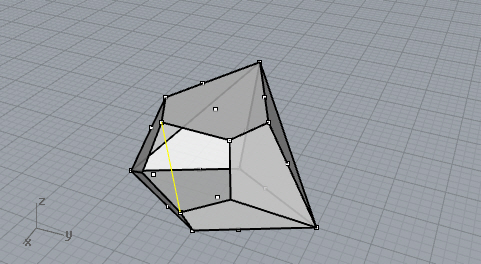
First cut,

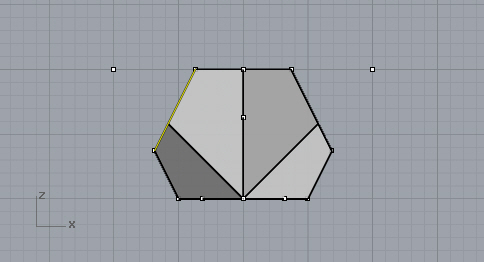
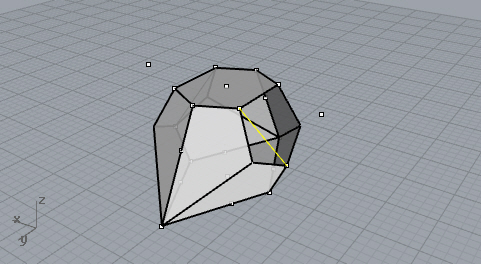
Second cut. Just draw a line, get to a side viewport, and trim the solid.

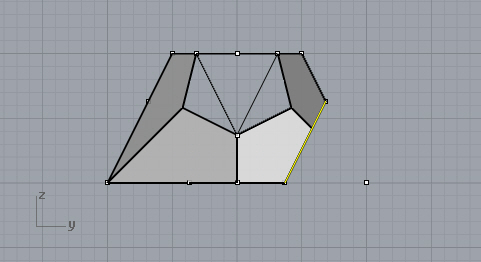
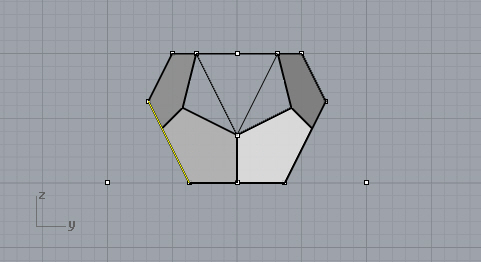
Third cut. This time, trimmed the rhombus below.

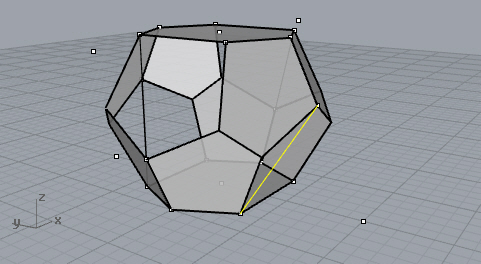
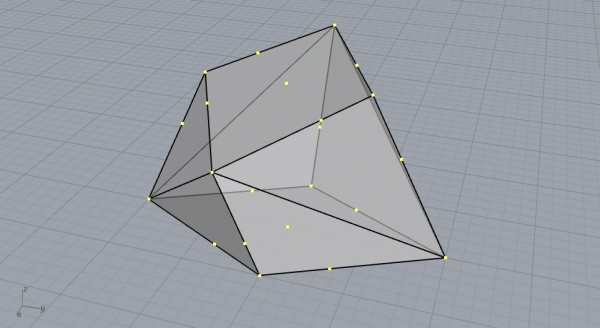
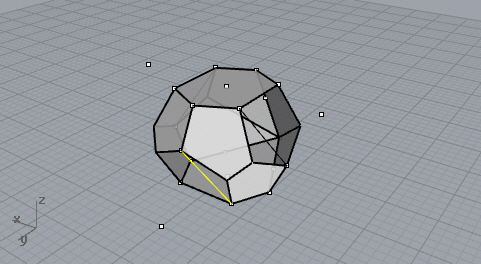
The fourth and final cut. Now cap the solid and finish the Tetrakaidecahedron.

Conclusion: The Weaire Phelan Structure

If you continue with the irregular dodecahedron, just place the 6 translating Tetrakaidecahedra properly, they’ll eventually emerge at irregular dodecahedron voids in between.

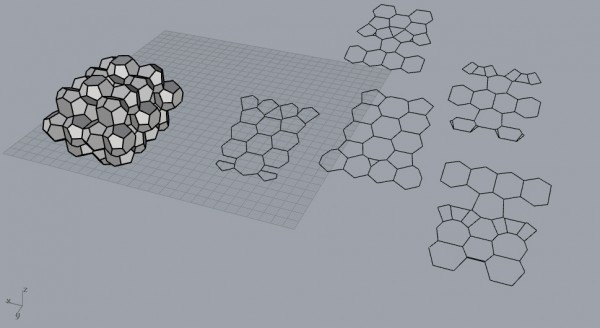
Finally, the bubble-like patterns start to emerge when I cut a packing of these objects with a slanted contour axis. If you had the patience to go this far, just pack them all, and rotate 3d them. Finally, cut with a rectangular prism to see a glimpse of the famous facade.

If you want to download and use the Rhino file; would you consider being my Patreon? Here is the link to my Patreon page[10] including the Rhino file for Tetrakaidecahedron and many other files.

Source URL: https://www.designcoding.net/weaire-phelan-structure/

---