Weaire-Phelan Structure

by Tuğrul Yazar | December 20, 2023 12:38

The Weaire-Phelan structure is an optimal solution to the problem of partitioning space into equal volumes with the least surface area. Denis Weaire and Robert Phelan discovered it in 1993. This structure gained attention due to its efficiency in filling space, offering a configuration that achieves a more balanced distribution of volume and surface area compared to other known structures at the time. Here is my model for Space-filling Weaire-Phelan Polyhedra.

The Weaire-Phelan structure consists of two different shapes; an irregular dodecahedron and a tetrakaidecahedron (14-sided polyhedra). These polyhedra fit together to form a foam-like structure with minimal surface area. Thus, this makes it a subject of interest in various fields, including materials science, physics, and mathematics. Additionally, architects and artists used it as a source of inspiration due to its aesthetically pleasing and unique geometric properties.

The Weaire-Phelan structure gained notable attention in the architectural realm with the design of the Beijing National Aquatics Center for the 2008 Summer Olympics in Beijing, China. This building is commonly known as the “Water Cube” (PTW Architects, CSCEC, CCDI, and Arup). It features an innovative bubble-like facade, similar to the Weaire-Phelan structure. The building’s exterior mimics the cellular structure made of a lightweight, translucent material called ETFE (ethylene tetrafluoroethylene).

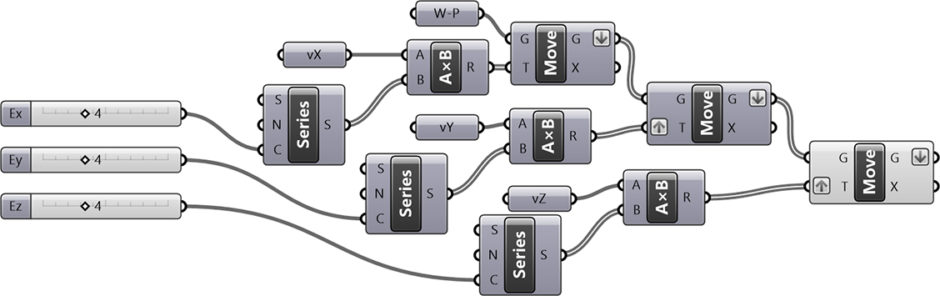
You can rebuild the Weaire-Phelan structure by following this link[1] for the construction of the tetrakaidecahedron. You will need to create an array of them to finish the structure. However, if you want to support me by downloading my Rhino and Grasshopper files; would you consider being a Patreon[2]? Thank you.

Source URL: https://www.designcoding.net/weaire-phelan-polyhedra/

---