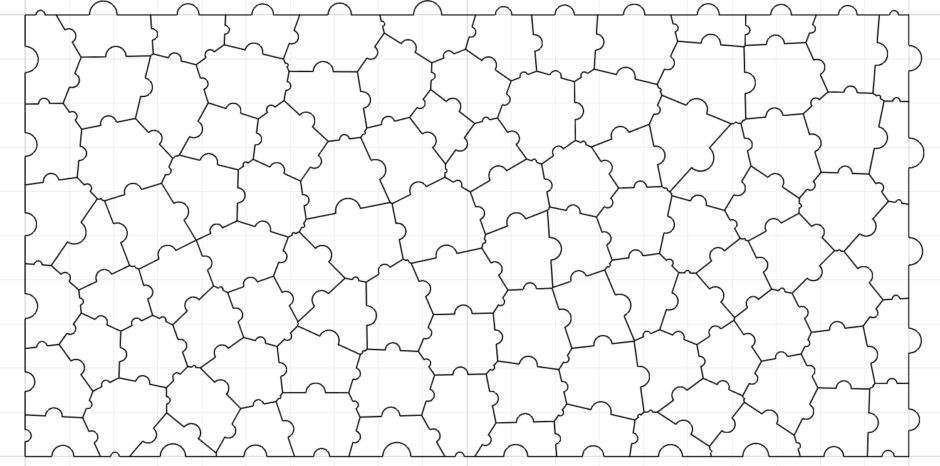
Voronoi Puzzle

In this Voronoi puzzle exercise, we derive two-dimensional puzzles by using Voronoi diagrams. This is similar to my previous studies here, and here.

Part 1: The Random Voronoi Diagram

In section 1 of the below image, I use a rectangular region to generate random points. Then, I create a standard Voronoi diagram by using those points. Finally, I explode the Voronoi cells.

Part 2: The Voronoi Puzzle Details

In the second part, we draw an arc on the edges of each cell. This makes the indentations and protrusions where the cells are interlocked. The parameters required to be able to draw the arc are the arc’s center point and radius and what angle it sweeps. This time we calculate the center point via a plane. Because the directions of all the flaps are different from each other. Each plane is placed at the midpoints of the edges. For this, it will be sufficient to enter the parameter 0.5 after reparameterizing all the exploded edges to the Evaluate Curve (Eval) component. The X input of each plane, that is the X axis, is connected to the T, or tangent vector, which comes out of the Evaluate Curve (Eval) component.

Notice that the X-axis, which is the red axis line of the symbols representing the planes, is parallel to the border lines of the cells. After giving the center point and one of the axes for a plane, the other axis will be the direction facing at 90 degrees.

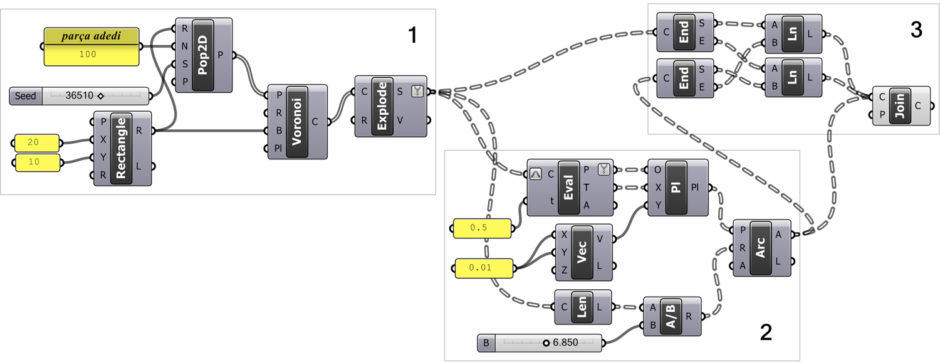
In this case, there are two possibilities for our Y-axes. These are the axes in the +90 or -90 direction to the current X. The value we will give to the Y input of our plane component determines this. We create a simple vector with the Vector XYZ (Vec) component and connect it to this input. Here you can set all planes to face the other way by entering a positive or negative number in X and Y. This will eventually replace all the indentations and protrusions.

Part 3: Trimming and Closing the Cells

Now that the planes we will draw our arcs are ready, we can switch to the radius value that we will connect to the R input of the Arc component. You can also set this value as a constant. In practice, a radius value is calculated as a certain ratio of each edge. The Length (Len) component, which calculates the length of the edges, helps in this work. Finally, input A of the Arc component has the default value range of “0 To Pi”. This value corresponds to a semicircle between 0 and 180 degrees.

In the third part of the application, we cut the edge lines (trim) with these arcs. There are components that perform trimming in the Grasshopper. It is often possible to do the cutting in different and easier ways. We obtain our points using the End Points (End) component, which gives the beginning and end points of both the sidelines and the arcs. Then we draw them again with a Line (Ln) component.

Final: Voronoi Puzzle

You can see what’s going on by closing the Previews of everything and just opening the Line (Ln) components. By using two Lines (Ln), we draw these lines on top of each other. But this allows the final Join Curves (Join) component to join each puzzle piece in a separate closed polyline. If you bake this component and examine it in Rhino, you can obtain the cells separately in every Voronoi Puzzle instance.