Vector Projection and Angle

by Tuğrul Yazar | December 21, 2021 00:23

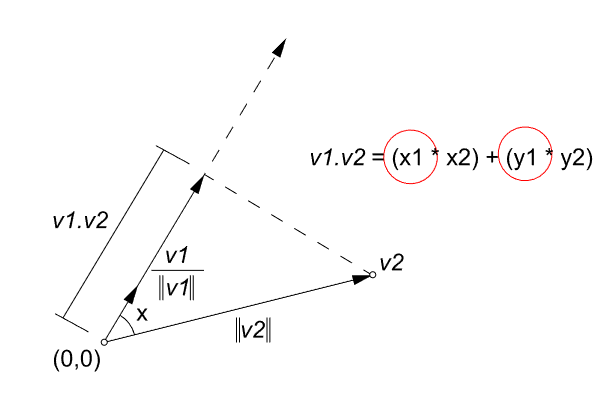
In this session, I will add two new methods to the Vector class. I think this will finish the basics for the vectors[1]. In the future, we are going to need several new methods like adding multiple vectors and interpolation. But for now, I think this would be sufficient to further advance into parametric curves [2]and surfaces. These new methods will be based on the dot product[3] method we created in the last post[4]. I will add the vector projection method first.

import rhinoscriptsyntax as rs
import math
class Vector:
	def __init__(self, point):
		self.components = point
	def display(self, origin=[0,0,0]):
		v = self.components
		tip = (v[0]+origin[0], v[1]+origin[1], v[2]+origin[2])
		line = rs.AddLine(origin, tip)
		rs.CurveArrows(line, 2)
	def magnitude(self):
		v = self.components
		result = v[0]**2 + v[1]**2 + v[2]**2
		return math.sqrt(result)
	def add(vA, vB):
		v1 = vA.components
		v2 = vB.components
		addition = (v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2])
		return Vector(addition)
	def multiply(self, s):
		v = self.components
		return Vector([v[0]*s, v[1]*s, v[2]*s])
	def reverse(self):
		return self.multiply(-1)
	def subtract(vA, vB):
		return Vector.add(vA, vB.reverse())
	def normalize(self):
		return self.multiply(1/self.magnitude())
	def dot(vA, vB):
		v1 = vA.components
		v2 = vB.components
		return v1[0]*v2[0] + v1[1]*v2[1] + v1[2]*v2[2]
	def project(vA, vB):
		vn = vA.normalize()
		pB = Vector.dot(vn, vB)
		return vn.multiply(pB)
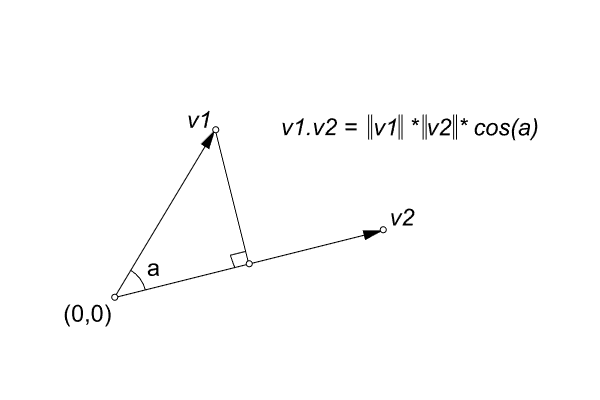
	def angle(vA, vB):
		vC = Vector.project(vA, vB)
		angle = math.acos(vC.magnitude()/vB.magnitude())
		if Vector.dot(vA, vB) < 0: angle = math.pi - angle
		return math.degrees(angle)

Below is a line-by-line explanation of the project and angle methods:

Line	Explanation
*1-32*	Already explained in the previous posts.
33	Define a new method called “project”. Take two vectors as inputs. So, this is not an instance method, but a general method of the class itself called a “class method”. This method will be called Vector.project()
34	Normalize the first input vector and store the result in vn
35	Run dot product method we developed earlier with the second vector and the normalized version of the first vector.
36	Multiply the resulting value of the dot product with the normalized vector to obtain a projection vector.
37	Define another class method called “angle”.
38	Use the newly defined projection method using the two input vectors.
39	Calculate the angle between the vectors by using math.acos method and dividing the magnitude of the projection vector to the magnitude of the second input vector
40	Check if the dot product is negative, then modify the resulting angle so that it gives the correct value.
41	Return the result after converting the radians to degrees for better visualization.

I am planning to write a book about these topics, explaining them much better than this.

Endnotes:

vectors: https://www.designcoding.net/?s=vector
parametric curves : https://www.designcoding.net/parametric-curve-equations/
dot product: https://www.youtube.com/watch?v=LyGKycYT2v0
last post: https://www.designcoding.net/vector-normalization-and-dot-product/

Source URL: https://www.designcoding.net/vector-projection-and-angle/