Vector Projection and Angle
In this session, I will add two new methods to the Vector class. I think this will finish the basics for the vectors. In the future, we are going to need several new methods like adding multiple vectors and interpolation. But for now, I think this would be sufficient to further advance into parametric curves and surfaces. These new methods will be based on the dot product method we created in the last post. I will add the vector projection method first.
import rhinoscriptsyntax as rs
import math
class Vector:
def __init__(self, point):
self.components = point
def display(self, origin=[0,0,0]):
v = self.components
tip = (v[0]+origin[0], v[1]+origin[1], v[2]+origin[2])
line = rs.AddLine(origin, tip)
rs.CurveArrows(line, 2)
def magnitude(self):
v = self.components
result = v[0]**2 + v[1]**2 + v[2]**2
return math.sqrt(result)
def add(vA, vB):
v1 = vA.components
v2 = vB.components
addition = (v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2])
return Vector(addition)
def multiply(self, s):
v = self.components
return Vector([v[0]*s, v[1]*s, v[2]*s])
def reverse(self):
return self.multiply(-1)
def subtract(vA, vB):
return Vector.add(vA, vB.reverse())
def normalize(self):
return self.multiply(1/self.magnitude())
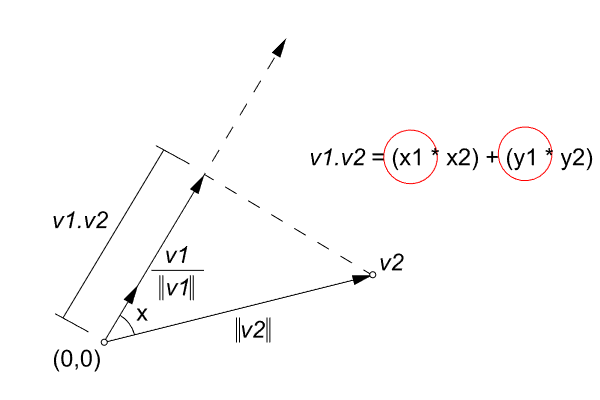
def dot(vA, vB):
v1 = vA.components
v2 = vB.components
return v1[0]*v2[0] + v1[1]*v2[1] + v1[2]*v2[2]
def project(vA, vB):
vn = vA.normalize()
pB = Vector.dot(vn, vB)
return vn.multiply(pB)
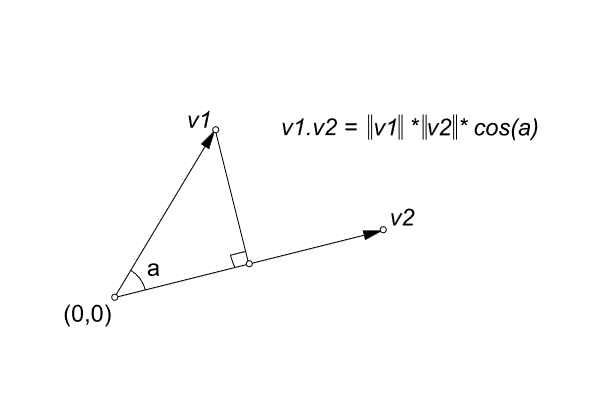
def angle(vA, vB):
vC = Vector.project(vA, vB)
angle = math.acos(vC.magnitude()/vB.magnitude())
if Vector.dot(vA, vB) < 0: angle = math.pi - angle
return math.degrees(angle)Below is a line-by-line explanation of the project and angle methods:
| Line | Explanation |
| 1-32 | Already explained in the previous posts. |
| 33 | Define a new method called “project”. Take two vectors as inputs. So, this is not an instance method, but a general method of the class itself called a “class method”. This method will be called Vector.project() |
| 34 | Normalize the first input vector and store the result in vn |
| 35 | Run dot product method we developed earlier with the second vector and the normalized version of the first vector. |
| 36 | Multiply the resulting value of the dot product with the normalized vector to obtain a projection vector. |
| 37 | Define another class method called “angle”. |
| 38 | Use the newly defined projection method using the two input vectors. |
| 39 | Calculate the angle between the vectors by using math.acos method and dividing the magnitude of the projection vector to the magnitude of the second input vector |
| 40 | Check if the dot product is negative, then modify the resulting angle so that it gives the correct value. |
| 41 | Return the result after converting the radians to degrees for better visualization. |
I am planning to write a book about these topics, explaining them much better than this.








