Vector Normalization and Dot Product

by Tuğrul Yazar | October 29, 2021 13:06

This is the continuation of the Vector class we started here[1], and further advanced here[2], here[3], and here[4]. This new Rhino Python[5] implementation is mostly educational and partially a hobby. Before this session, we have developed display, magnitude, add, multiply, reverse, and subtract methods. This time, I am adding the vector[6] normalization and dot product methods and seeing the utilizations of the dot product.

import rhinoscriptsyntax as rs
import math
class Vector:
	def __init__(self, point):
		self.components = point
	def display(self, origin=[0,0,0]):
        v = self.components
        tip = (v[0]+origin[0], v[1]+origin[1], v[2]+origin[2])
        line = rs.AddLine(origin, tip)
        rs.CurveArrows(line, 2)
	def magnitude(self):
		v = self.components
		result = v[0]**2 + v[1]**2 + v[2]**2
		return math.sqrt(result)
	def add(vA, vB):
		v1 = vA.components
		v2 = vB.components
		addition = (v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2])
		return Vector(addition)
	def multiply(self, s):
		v = self.components
		return Vector([v[0]*s, v[1]*s, v[2]*s])
	def reverse(self):
		return self.multiply(-1)
	def subtract(vA, vB):
		return Vector.add(vA, vB.reverse())
	def normalize(self):
		return self.multiply(1/self.magnitude())
	def dot(vA, vB):
		v1 = vA.components
		v2 = vB.components
		return v1[0]*v2[0] + v1[1]*v2[1] + v1[2]*v2[2]

Line	Explanation
*1-26*	Already explained in the previous posts.
27	Define a new method called “normalize”.
28	Call the multiply method for the given vector (self), with the scalar of 1/magnitude. This will reduce the length to 1. Imagine a vector with a length of A. Multiplying it with 1/A would result in 1.
29	Define a new class method called “dot”. This method takes two vector objects.
30	To make the code lines shorter, create a temporary variable called v1 and store the components (list of three numbers) of the first input vector.
31	Create a temporary variable called v2, and store the components (list of three numbers) of the second input vector.
32	Calculate the dot product (which is a single number) and return it to the user whenever it is called

In the above code, I created a new method for vector normalization, called normalize(). Since we developed a vector-scalar multiplication method earlier, now we can use it to reduce (or increase) the magnitude (length) of any vector to 1 unit. Therefore, the method multiplies the given vector by 1 / its magnitude.

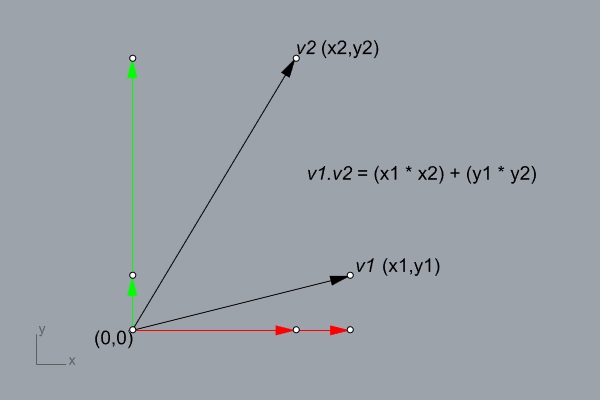
Then, I developed a simple dot product method. The above diagram shows the formula for two-dimensional vectors. Therefore, you can generalize it to n-dimensional vectors by the same formula. Finally, to have a good insight on the dot product I highly recommend watching this[7] and this[8].

Endnotes:

here: https://www.designcoding.net/vector-class-in-rhino-python/
here: https://www.designcoding.net/vector-arithmetics-in-rhino-python/
here: https://www.designcoding.net/more-vector-operations-in-rhino-python/
here: https://www.designcoding.net/vector-magnitude-method-in-rhino-python/
Rhino Python: https://www.designcoding.net/category/tools-and-languages/rhino-python/
vector: http://vector
this: https://www.youtube.com/watch?v=LyGKycYT2v0&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=10
this: https://www.youtube.com/watch?v=2PrSUK1VrKA&t=13s

Source URL: https://www.designcoding.net/vector-normalization-and-dot-product/