Vector Normalization and Dot Product
This is the continuation of the Vector class we started here, and further advanced here, here, and here. This new Rhino Python implementation is mostly educational and partially a hobby. Before this session, we have developed display, magnitude, add, multiply, reverse, and subtract methods. This time, I am adding the vector normalization and dot product methods and seeing the utilizations of the dot product.
import rhinoscriptsyntax as rs
import math
class Vector:
def __init__(self, point):
self.components = point
def display(self, origin=[0,0,0]):
v = self.components
tip = (v[0]+origin[0], v[1]+origin[1], v[2]+origin[2])
line = rs.AddLine(origin, tip)
rs.CurveArrows(line, 2)
def magnitude(self):
v = self.components
result = v[0]**2 + v[1]**2 + v[2]**2
return math.sqrt(result)
def add(vA, vB):
v1 = vA.components
v2 = vB.components
addition = (v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2])
return Vector(addition)
def multiply(self, s):
v = self.components
return Vector([v[0]*s, v[1]*s, v[2]*s])
def reverse(self):
return self.multiply(-1)
def subtract(vA, vB):
return Vector.add(vA, vB.reverse())
def normalize(self):
return self.multiply(1/self.magnitude())
def dot(vA, vB):
v1 = vA.components
v2 = vB.components
return v1[0]*v2[0] + v1[1]*v2[1] + v1[2]*v2[2]| Line | Explanation |
| 1-26 | Already explained in the previous posts. |
| 27 | Define a new method called “normalize”. |
| 28 | Call the multiply method for the given vector (self), with the scalar of 1/magnitude. This will reduce the length to 1. Imagine a vector with a length of A. Multiplying it with 1/A would result in 1. |
| 29 | Define a new class method called “dot”. This method takes two vector objects. |
| 30 | To make the code lines shorter, create a temporary variable called v1 and store the components (list of three numbers) of the first input vector. |
| 31 | Create a temporary variable called v2, and store the components (list of three numbers) of the second input vector. |
| 32 | Calculate the dot product (which is a single number) and return it to the user whenever it is called |
In the above code, I created a new method for vector normalization, called normalize(). Since we developed a vector-scalar multiplication method earlier, now we can use it to reduce (or increase) the magnitude (length) of any vector to 1 unit. Therefore, the method multiplies the given vector by 1 / its magnitude.
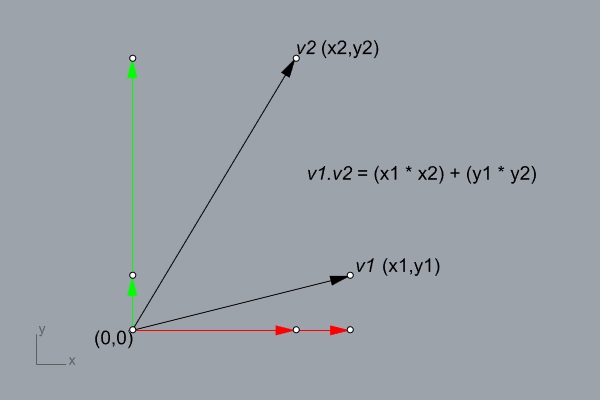
Then, I developed a simple dot product method. The above diagram shows the formula for two-dimensional vectors. Therefore, you can generalize it to n-dimensional vectors by the same formula. Finally, to have a good insight on the dot product I highly recommend watching this and this.








