Vector Magnitude Method in Rhino Python
by Tuğrul Yazar | October 12, 2021 09:14
Today, I am going to make only one addition to the Vector[1] class we recently started[2] in Rhino Python[3]. The magnitude of a vector can be easily calculated by assuming that the axes (2 or 3 axes) of it are perpendicular to each other. This gives us an opportunity to assume a right triangle visually, and calculate the magnitude (length) of a vector by using the Pythagorean Theorem[4]. In short, if you square and add the components of a vector, and then take the square root of this, you will get the hypotenuse of the right triangle, which is the magnitude of the vector, represented by those components.
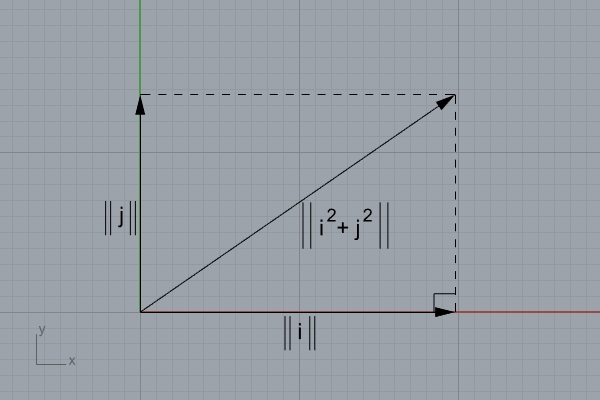
Don’t mix the vector addition with today’s topic. Because as you know from previous posts, a vector can be represented by the addition of its components. So, we can identify these components as “i” and “j”. These represent the 1D building blocks of our 2D vector. When we add i and j, we find the resulting vector’s tip point. However, to find the magnitude of this vector, we cannot just add up the lengths of i and j. As you see in the image, this process is on a 2D space, rather than a 1D number line. Therefore, seeing the geometric intuition behind this method is important. Here is the Rhino Python code that mimics the above process:
Rhino Python Implementation of Vector Magnitude
import rhinoscriptsyntax as rs
from math import *
class Vector:
def __init__(self, point):
self.components = point
def display(self, origin=[0,0,0]):
v = self.components
tip = [v[0]+origin[0], v[1]+origin[1], v[2]+origin[2]]
line = rs.AddLine(origin, tip)
rs.CurveArrows(line, 2)
def magnitude(self):
v = self.components
result = v[0]**2 + v[1]**2 + v[2]**2
return sqrt(result)| Line | Explanation |
| 1-10 | Already explained in previous posts, except line 2, which imports the methods of the built-in math module. This will be used to call the square root (sqrt) method in the last line. |
| 11 | Define a new method called “magnitude”. |
| 12 | Get the components of the vector. |
| 13 | Define a new variable called “result” and calculate the square (** is the power function in Python) of each component and add them up. This should work for both 2D and 3D vectors. |
| 14 | Return the square root of the result variable. |
Testing the code
Finally, to see this code in action, you can test it with various vector objects. For example, you can add the below code and run:
myvector = Vector([4,5,0])
myvector.display()
print(myvector.magnitude())- Vector: https://www.designcoding.net/tag/vector/
- started: https://www.designcoding.net/more-vector-operations-in-rhino-python/
- Rhino Python: https://www.designcoding.net/category/tools-and-languages/rhino-python/
- Pythagorean Theorem: https://en.wikipedia.org/wiki/Pythagorean_theorem
Source URL: https://www.designcoding.net/vector-magnitude-method-in-rhino-python/