Variable Voronoi Study

by Tuğrul Yazar | November 30, 2012 11:02

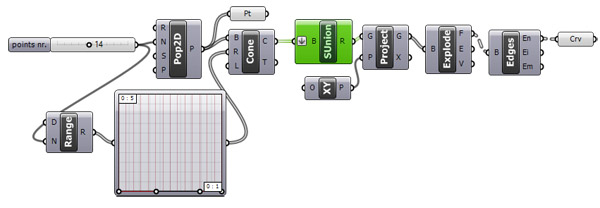
I’ve been searching for a method to study the Voronoi subdivision in order to manipulate it. There are well-known algorithms for that. But I thought it would be better if I use a projective approach just as I did in studying hyperbolic space (here[1]). This is the metaphor of inflating balloons. However, I inflated cones instead of spheres. This way, it became possible to modify the algorithm. So I was able to develop a kind of variable Voronoi study here. Of course, it is not a real Voronoi because the edges are not straight.

Above is the regular Voronoi subdivision in 5 steps, with constantly and equally inflating points. As a result, the code is very simple and easy to use. It is a good educational experiment on the usage of projections and intersections in native Grasshopper.

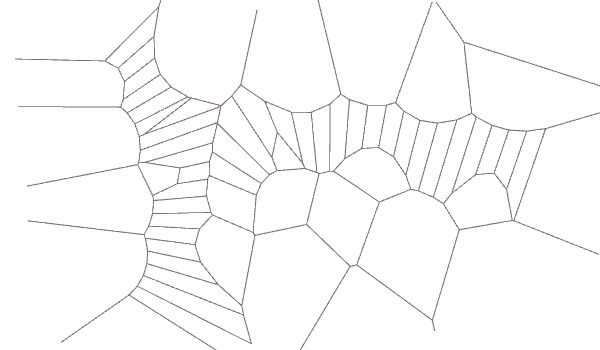
The second attempt (above) shows an interpretation of the variable Voronoi study. Again I inflated points at variable distances. Curved edges are because of different cone heights. You can study linear edges by manipulating those heights to be the same.

And finally, I tried to put attractor curves, in addition to points in this algorithm. Thus I put spheres instead of cones. Look what happened;

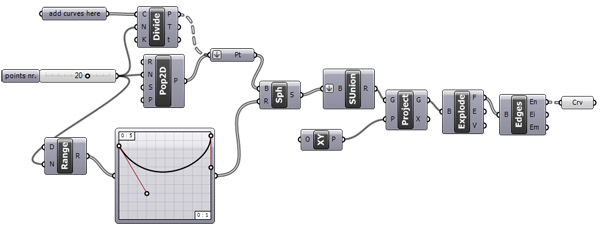
Straight edges and variable effect from each point. Here is the working Rhino 5 Grasshopper file from 2012. This code still works in 2021. Because it was made by using the native Grasshopper components. This makes the code more durable, simple, and educational.

Here[8] is a link that inspired me to this study. This post could be further improved by studying various components and sweeping objects along curves.

Source URL: https://www.designcoding.net/variable-voronoi-study/

---