Trees and Recursive Computing

by Tuğrul Yazar | March 15, 2012 17:12

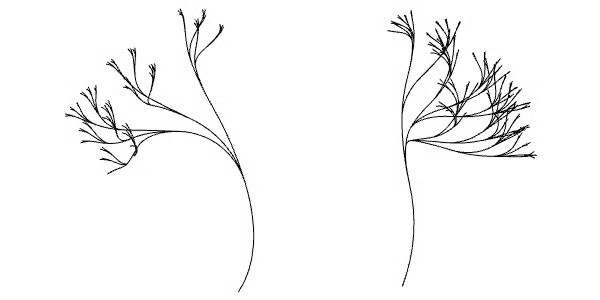
This topic of trees and recursive computing is inspired by the method shown here[1] at the Rhino Python 101 Primer. This is a beautiful method of recursion that creates tree-like shapes, composed of arcs. I constructed these arcs by using the Arc SED (start, end, direction) method. This requires start and end points and a vector that is tangent to the arc (at the start point). Therefore, the overall look of a chain of these constructions creates curves with continuous curvatures, as every arc is tangent to the previous one. However, I cannot simulate such constructions in Grasshopper without any looping component. Because it defines the new arcs using the previous one.

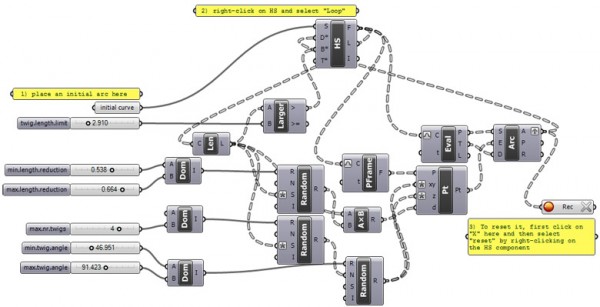
There are sliders defining maximum and minimum values to particular parameters of the tree, and a length limit, that says “stop” to Hoopsnake when necessary. These parameters are different from the ones in the original Python script, so the outputs are also different. Recursion starts with the initial curve you’ve defined in Rhino. Then, Grasshopper takes its endpoint and corresponding tangent vector to start the iterations. I rotate each twig around the vector at a random angle (defined by min-max values). I also shortened them by using a random factor. After drawing arcs these twigs are then fed back to Hoopsnake. Then, the same loop creates new ones using the same procedure.

You can rebuild the definition by looking at the definition image, and the explanation above. Here[3] is the Hoopsnake add-on necessary for this. However, if you liked this content and want to support this website by downloading my Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[4] including the working Grasshopper files for the Trees and Recursive Computing, and more.

Source URL: https://www.designcoding.net/trees-and-recursive-computing/

---