The Moebius Strip

by Tuğrul Yazar | January 18, 2012 00:27

A Moebius strip, also known as a Moebius band, is a fascinating mathematical object and a type of non-orientable surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in the 19th century. To visualize a Moebius strip, imagine taking a long, narrow strip of paper and giving it a half twist before connecting its ends to form a loop. The result is a surface with only one side and one edge.

This Grasshopper definition generates a parametric Moebius strip with a thickness parameter input. Inspired by the works of Andrew F. Scott, (here especially[1]). I decided to create a parametric Moebius strip model used as a foundation for various sculpture projects and educational exercises. The most challenging part of this problem was creating a single surface (not a Brep) to process it easier later on. The construction process of the model starts with a 3D ellipse, divided into equal distances. Then, I created new ellipses at each division point over specific planes. I duplicated the first ellipse. Then I put it at the end of this list to create an illusion of the continuous surface. After all, the Loft component generates the surface. Further experiments on this model could include the fabrication of this model.

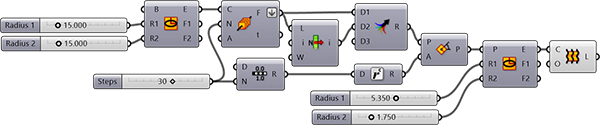
You can rebuild the definitions by looking at the diagram and the tutorial[2] video. However, if you want to support this website by downloading my Grasshopper files; would you consider being my Patreon? Here is the link to my Patreon page including the working Grasshopper files for the Moebius Strip and more. 

Source URL: https://www.designcoding.net/the-moebius-strip/

---