The Golden Ratio in Grasshopper

I like to deal with possible small computational geometry problems. These fun games are taking 2-3 hours. In addition, these are also memorable exercises. I was reviewing the Anemone plugin last week. I noticed that the Golden Ratio in Grasshopper was not geometrically generated before.

Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. … Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.

Mario Livio (via Wikipedia)

At first, it seems very easy. But this problem has kept me busy for a while. We must rotate and copy squares around changing center points. Thus, we can use this method to calculate the golden ratio, which is the ratio between the long and short edges of the rectangles generated by this procedure. I could only do this by adding a rotation pattern. Therefore, it can work with any closed polygon.

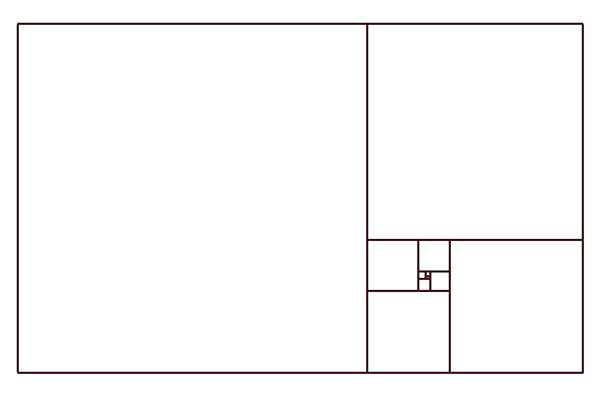
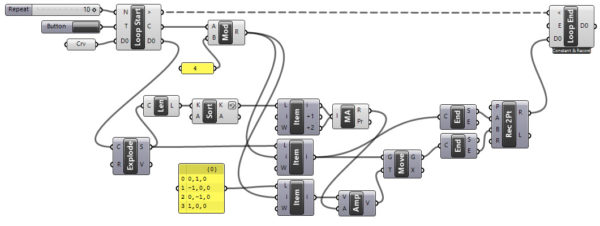
Above, I presented the construction of the Golden Ratio in Grasshopper. I tried to implement it via the repeating rotation pattern of squares. I defined an iteration number in Anemone. So the process can continue many times. This is an open definition for further development. For instance, we can draw the Golden Spiral. I checked the code in Rhino 7. I think the looping should be a standard feature of Grasshopper.