Construction of Tetrahedron

by Tuğrul Yazar | December 19, 2011 23:31

The tetrahedron is a platonic solid with 4 equal triangular faces (which are also equilateral), 6 equal edges, and 4 vertices. While creating this shape, we will take a closer look at length transfers using compass-like tools both in two and three-dimensional space.

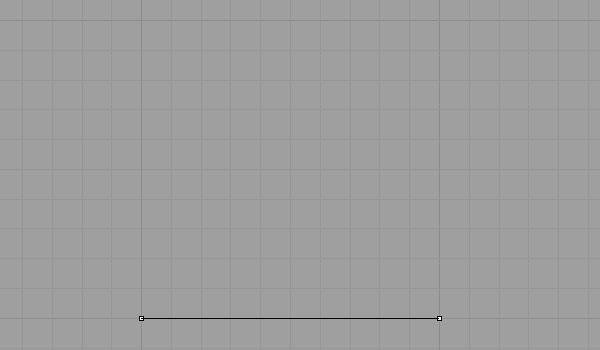
In order to define the edge length of the first triangle (which is a straight line), start with any two points in cartesian space.

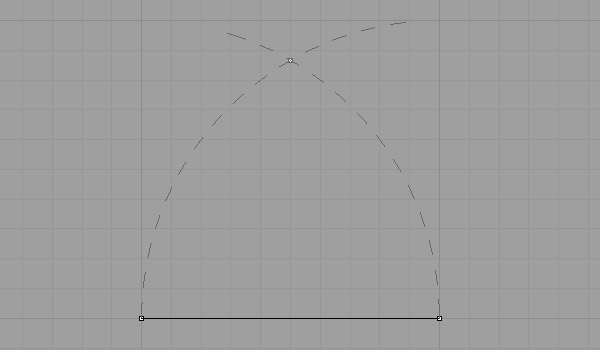
Using a compass (arc or circle), draw two arches (or circles) using your initial points as corners, and the distance between your points as radius. Now you’ve found the third corner of your equilateral triangle, at the intersection of these arches.

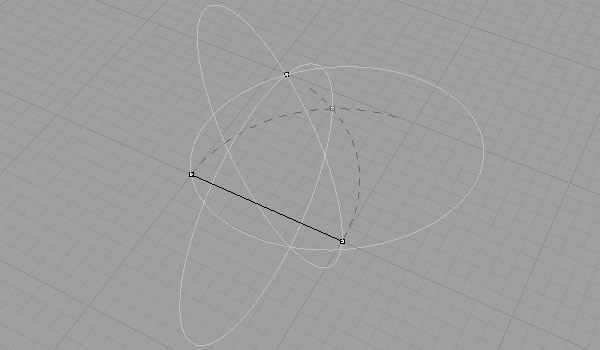
This time, do the same thing in three dimensions. Imagine the fourth and last corner point of the tetrahedron above your triangle. As all faces of the tetrahedron are equilateral triangles, this point has to be at the same radius distance you’ve determined above. However, you’ll be using a three-dimensional compass (or a sphere) to transfer this distance and find the intersection of equal distances to these three corners. If you intersect only two spheres, you’ll find a circle. This means the fourth point you are looking for lies in this circle. You need the third sphere to be intersected with the circle, to find the exact location of the fourth corner located on the circle.

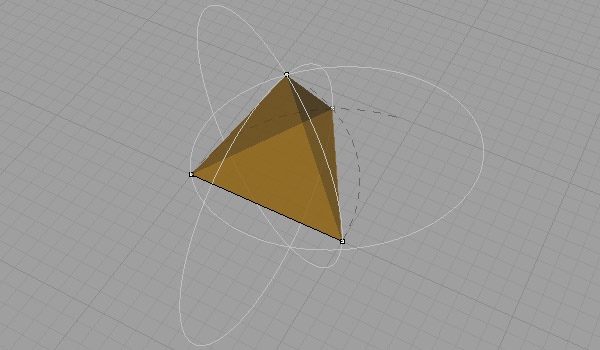
Create triangular faces of the tetrahedron using these four corner points. Below is a video, explaining the process:

Source URL: https://www.designcoding.net/tetrahedron/

---