This is the six-pointed star lattice definition in Grasshopper. The definition is generating CNC or laser-ready results as seen below. In this code, first, I developed a common star pattern by exploding a hexagonal grid. The tricky part of this definition is the last part. There, you can see how you can use the Region Union (RUnion) component to add thickness to a pattern we have drawn before. The operation […]

Here is the abstract of my last publication in the International Journal of Architectural Computing. Parquet Deformations is an architectural studio exercise of William Huff in the 1960s. It aims to improve students’ reasoning of spatiotemporal variation by utilizing sequential shape-shifting of patterns. This article examines the outcomes of this educational research from the perspective of design computing. A multilayered reading about the exercise will reveal its historical, theoretical, and artistic backgrounds. Then […]

This is one of the ideas we’ve tested for the workshop “Animate Patterning“. Inspired by this work, Apart from the pattern that turns around, the torque, rotation radius and speed of the servo, weight, connection detail, and a number of foamboards become important inputs for this design. In the three-day workshop, one group of students interpreted this idea of using several moving layers and creating an emergent pattern at the […]

Basic Design I exercise called “Cut and Fold: Deviation” explores diversity within relationships and material behavior. It is initially introduced by Salih Küçüktuna as a simple but effective exercise platform. Below are some students’ works on this one-week exercise. The term “deviation” has many uses in a range of fields from medicine to sociology. However, it is frequently used in statistics with an interesting evocation to design computing: In mathematics […]

I’ve come across this nice website about the short history of tilings and tessellations. In this post, I am regenerating a tiling of Dürer rhombii. Albrecht Dürer sounds like one of the pioneers of some of the concepts of today’s emerging field of architectural geometry. Here is a phrase from that website about Dürer; “…Like Kepler, regular polygons and polyhedra fascinated Dürer… A large section of the Painter’s Manual is dedicated to […]

Below is some student works from this year’s Architectural Geometry / Pattern Deformations assignment. Students developed their own pattern deformation sequences mostly on regular tessellations. Based on the classical Parquet Deformation exercise, we tried to implement a rule-based approach in order to explore emergent patterns. The exercise seems to reveal endless improvisation potential. The exercise requires students to design a pattern deformation on a 28cm by 28cm area. It should […]

For the last 10 days, I’ve been searching for a proper algorithm for representing surfaces using planar shapes. It is obvious that triangulation is an answer but there is an interesting research topic of planar remeshing using shapes other than quads, hexagons, or any other regular polygons. Especially in computer graphics, such things refer to the optimization of models to decrease the load of GPUs. In the Grasshopper community, this […]

It all started with my new passion for origami tessellations, not much of origami, but the tessellation part. I was too lazy to fold it physically, nor model them using an engine such as Kangaroo. That would also be very unnecessary (and yes, very boring) to simulate a folding effort on the computer unless we lose our connection with the real world. Instead, I tried to look at a much […]

I’ve been searching for a method to study the Voronoi subdivision in order to manipulate it. There are well-known algorithms for that. But I thought it would be better if I use a projective approach just as I did in studying hyperbolic space (here). This is the metaphor of inflating balloons. However, I inflated cones instead of spheres. This way, it became possible to modify the algorithm. So I was […]

In this exercise, we asked students to develop a method to produce custom tessellations. This is based on the analysis of what is called “Islamic patterns”. We have discussed Eric Brough‘s famous book “Islamic Geometric Patterns”, regarding geometric relationships and linear connectivities via underlying tessellations (such as regular square and hexagonal). Thus, this geometry and drawing exercise is called “Seamless Patterns” in the Design Geometry course at İstanbul Bilgi University. […]

Last week, the first-year architectural geometry course was about pattern deformations. Students are expected to familiarize themselves with 2d drawing, transformation, and control point editing commands while trying to design a deformation. After studying regular and semi-regular tessellations of the plane, they are expected to develop reasoning on the rule-based and iterative processes. This also constructed an underpinning for Basic Design‘s “Metamorphosis” study, where they have discussed more conceptual frameworks […]

This is not to explain the method of the Parquet Deformation but to see the potential. After we’ve studied regular, semi-regular, dual, and truncated tessellations with students, the Architectural Geometry course expects them to develop a Parquet Deformation handmade such as those shown below. I call them Parquet Deformation handmade. Because they are manually designed but drawn using traditional CAD. The samples you see below are from this website. It […]

We can create tessellations of outer points in a Poincare Disk, using the manual method explained in the last post (here). But repeating that compass and straightedge process is becoming a little useless after a couple of repeats. If you say “ok. I understood the concept, let’s get faster!” then we can model just the same process in Grasshopper3D to examine varying results in seconds; If we connect any grid of […]

Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]

Creating and handling new types of grid configurations might be an important topic, as Grasshopper is not supporting them natively (yet). I tried to create some semi-regular tessellations based on regular grids. It is actually truncated versions of regular grids, but it slowly becomes interesting as I realized that I may further truncate emerging grids to create Level 2 and Level 3 grids with more complex tessellations. Here are two […]

As far as I understood, it is impossible to physically construct double-curved surfaces from quadrilateral and planar faces. This definition tries to find an optimized alternative to this problem. Any surface, single or double curved, is divided into standard sub surfaces. But this time, those surfaces are treated as planar surfaces, therefore one corner is moved to meet this requirement. The output consists of only planar surfaces ready for fabrication. […]

After Puzzling, I tried to establish more of Escher’s basic grid transformations using Grasshopper’s native components. This definition simulates Escher’s transformation of four-cornered grids. The postulate is based on the fact that every quadrilateral (or triangular) planar shape can create regular tessellations without gaps or overlaps. In the traditional method, this tessellation is achieved by rotating the shape 180 degrees and copying afterward. However, in Grasshopper we simply define the […]

Nowadays, I found myself back into traditional hand sketching. Several failed attempts on Grasshopper led me back there. NURBS (and Grasshopper) somehow limits our conception of surfaces to four-cornered (or two-directional) manifolds. Although it sounds like limiting our designs, having four-cornered component spaces has still lots of experimental fields for designers. Escher is a cult person, who transforms the euclidean coordinate system to meet his design intentions. There are lots […]

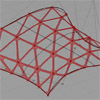
This is the old-method Parametric Truss definition. Interestingly this quickly became a solid solution, used and taught for years. I couldn’t find a better answer yet. As Grasshopper updates, some of the components in this definition change but the overall structure remains. Subdivision of a free-form surface and addition of geometric components has, of course, a wide range of alternatives. Maybe we should combine this with different problems and solutions […]

This is another starting point for pattern generation study in a dataflow environment. I tried to implement the parquet deformation of Islamic patterns in Grasshopper. I studied Hankin’s method of Islamic Pattern generation. Then I tried to simulate his process beginning with basic regular tiling (regular hexagonal tessellation). Craig S. Kaplan (here) explains this and other methods in his dissertation. A Simple Foundation We have already experienced the result of […]