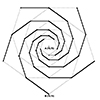
A spiral is a curve that begins at a central point and continuously moves outward, either getting larger (in an outward spiral) or smaller (in an inward spiral). It often revolves around a central point or axis. Spirals are fascinating because they appear in many aspects of nature, mathematics, and art. In this drawing exercise, I utilized several commands to draw such a system. However, this drawing is not a […]

“In the heart of a sunflower’s embrace, its seeds weave a poetic tale—a dance of two spirals, parastichies they’re called. One unfurls gracefully from the center in the hush of clockwise whispers, while its counterpart whispers secrets in the tender breaths of counterclockwise motion. A subtle ballet unfolds, where the number of these spirals gracefully mirrors the whispers of adjacent Fibonacci numbers, composing a delicate symphony in the sun-kissed fields.” […]

The final countdown has started until the jury of this semester’s Basic Design studio. Everyone is excited to see the products of this year’s architecture, interior design, and industrial design students, while they are trying to set a higher standard for the exercise.  They’ll use both digital and physical media to unfold their design intentions about a systematic whole. Below is the current situation of our group together with Fulya […]

Grasshopper still surprises me. This definition draws a spiral by using a random component. It is obvious that the seed value of the random component has a relationship with an archimedean or a similar spiral. My intention was to create a definition to put a number of random points inside a circular area, not a rectangular one. While I grow the radius of a circle and get a t parameter […]

In this exercise, Grasshopper draws various Archimedean spirals. It constructs polar points and maps them onto a range of angles and a number of points. The spiral’s turning speed is determined by the constant “a,” while the constant “n” gives unique names to the spirals by raising the angle variable to the power of 1/n. Wolfram Mathworld names the spiral with n = -2 as lituus, n = -1 as […]

Sunflower Spiral (or Phyllotaxis) can be constructed in Grasshopper according to Vogel’s model of parametric relationships. This model uses polar coordinates. You can download the Grasshopper definition file here: (The Grasshopper file is still working after more than 11 years -15.12.2022. This is such a powerful quality of Grasshopper, I think.) It’s a good example of utilizing polar coordinates. It’s also fun to play with the parameters and constraints of […]