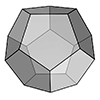
This is a 3d modeling tutorial for the platonic solid of dodecahedron. Modeling a dodecahedron is a good exercise for the basic transformation commands such as Rotate3D in Rhinoceros. You will see that it is possible to calculate the rotation angle by using sphere intersections. I learned this elegant method while teaching Architectural Geometry classes 12 years ago. It is based on the fact that, given a rotation axis and […]

This website explains the problem and several solutions. I managed to implement the formulas to convert a 2D square grid into spherical coordinates. The Fibonacci Sphere is one of the solutions to the equal distribution of points on a sphere. It is not the best solution to this problem. But it is regarded as a quick and efficient one. Suitable for me. I developed this Grasshopper code by studying the […]

According to Wolfram, “By the duality principle, for every polyhedron, another polyhedron exists in which faces and polyhedron vertices occupy complementary locations. This polyhedron is known as the dual, or reciprocal”. We can use this method to generate new polyhedra from known ones. I tried to develop a Dual Polyhedra Generator in this Rhino Python script. First, the script asks a user to select a closed polysurface object. Then, it […]

This was a couple of weeks ago, together with my six-year-old son Mete, we decided to make a “ball” out of old memory cards. I was curious about a subdivision method, using only planar quadrilaterals to construct a sphere (named Sixty Square Sphere. There are a couple of models on www. Of course look much better than mine:=). However, my son was expecting a “ball” to play. Then, both of […]

This is the second year we are experimenting with a beautiful exercise with the Computation-based Basic Design 1 students at İstanbul Bilgi University Faculty of Architecture. The exercise is based on the ideas of Benay Gürsoy and Şebnem Yalınay, who are among the pioneers of this studio. The exercise is about the design and production of new year’s lanterns to be lit in the campus garden. Here are a few […]

Today’s Architectural Geometry course was about platonic solids and different attractor objects in introducing component-based design systems. Benay’s idea was both pedagogical and interesting to test in Grasshopper. I searched for the most fundamental type of attractor solid in creating a composition such as this; There is a subdivided sphere and an attractor sphere. The pull component works great here. You may use multiple attractor solids or different shapes such […]

Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

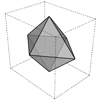
The tetrahedron is a popular platonic solid for designers. We’ve explained how to draw them using equilateral triangles here before. Recently I’ve found (sorry, lost the web address) a much quicker way of modeling a Tetrahedron using a cube. It’s very simple, just connecting the three opposite corners of the cube automatically makes them equal, resulting in the four equal faces. Of course this time you’ll have to calculate the […]