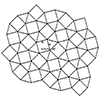
Snub Square Tiling is a semi-regular tessellation of the plane, composed of two squares and three regular triangles at each vertex. The arrangement of these two regular shapes seamlessly covers the plane without any gaps or overlaps. It is one of the eight semi-regular tessellations known in geometry. The dual of Snub Square Tiling is Cairo Pentagonal Tiling, which we will explore later. In this short tutorial, I am drawing […]
This is a late update for my 2012 study on Cairo Pentagonal Tiling (or Cairo Tessellation). Originally, it was an exercise of dual tessellations. Because this tiling is the dual of the famous semi-regular tessellation of Snub Square. After coding the Snub Square tiling, I attempted to generate the dual of it. However, that created an inefficient result. This latest version generates the original Snub Square and Cario Pentagonal Tilings. […]
Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral […]
