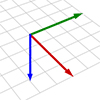
In the Digital Fabrication course, I needed to explain the plane orientation and rotation angles. This is why I prepared this Spatial Recognition Test. This is an important topic regarding the matching of the TCP (tool center point) plane of the robot and the plane(s) designers generate. In Rhino, we define a construction plane by red (X), green (Y), and blue (Z) colors. The relative positions among those axes are […]

Today, we started learning Robots add-on for Grasshopper. The first two codes we experimented with were similar to the first week’s jogging exercises. In the first one called “axial jogging”, we had 6 number sliders to control the angles of the axes. Every number slider generates values between -Pi and +Pi. These numbers are joined into a text by adding a comma in between. Then, Create program and Simulate Program […]

This is based on my failure of creating an optimum solution for planar polygonal subdivisions. There is a method called Tangent Plane Intersection (TPI), explained briefly here (sometimes similar algorithms are called “planar remeshing” and  “variational shape approximation”) which is effectively used in the Trada pavilion (here). I tried to implement a similar method using only native Grasshopper components and no recursion, but it quickly became much more complicated than […]

For the last 10 days, I’ve been searching for a proper algorithm for representing surfaces using planar shapes. It is obvious that triangulation is an answer but there is an interesting research topic of planar remeshing using shapes other than quads, hexagons, or any other regular polygons. Especially in computer graphics, such things refer to the optimization of models to decrease the load of GPUs. In the Grasshopper community, this […]

This experiment is based on a traditional surface-component definition. However, the variation of components is associated with Gaussian curvature. We just control the subdivision and a multiplier value. Results are interesting in as an educational tool to explain NURBS surface curvature and its utilization for Design Geometry. Different surface shapes generate exciting results. Of course, this could be much improved by recognizing positive and negative curvature values, (probably only accepting […]