Unlike the classical Pattern Deformations assignment discussed here and here, this time we asked Design Geometry students in 2014 to explore deformations by using referential systems as a secondary space. We wanted them to create variations on a regular pattern only by deforming its underpinning lattice. Below are three examples of this alternative assignment. I’m thinking about improving this exercise to three dimensions, seems possible to implement by using the cage […]

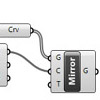
In today’s drawing class, we taught methods of drawing basic transformations by hand. Mirror was one interesting subject of that. However, then I opened Grasshopper and Rhino to test the effects of curved mirror planes. Unfortunately, I realized that there is already a curved mirror component in Grasshopper :( Here is the Grasshopper definition: [GHX: 0.9.0061] This might be one of the simplest ways of introducing generative deformations for design […]

The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear […]

Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]

[GHX: 0.8.0066] This is my second attempt on getting into non-euclidean representations of space. Althouth it seems easy at first sight, this represents a close point of theory between mathematics and contemporary computational design geometry. As always, architects tend to use mathematical terms such as “non-euclidean geometries” but as far as I saw, most of them have no idea about what it is. So, I’m trying to learn and understand this […]

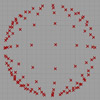
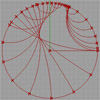
This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made […]