Stellation of polyhedra refers to the process of extending the faces (or edges) of a polyhedron outward to form new, more complex shapes. These new shapes, called stellations, are created by adding extra vertices, edges, and faces that “project” outward from the original polyhedron’s structure. You can create an infinite number of new polyhedral forms, depending on how you extend the faces and edges. In this short tutorial video, I […]

A dual polyhedron is a concept in geometry where two polyhedra are related in such a way that the vertices of one polyhedron correspond to the faces of the other, and the faces of the first polyhedron correspond to the vertices of the second. The process of creating a dual polyhedron is called duality, and it applies to many regular, semi-regular, and some irregular polyhedra. In the case of Platonic […]

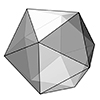
An icosahedron is a three-dimensional polyhedron with twenty triangular faces, twelve vertices, and thirty edges. It is one of the five Platonic solids and is highly symmetrical, with all faces being equilateral triangles. A regular icosahedron has equal edge lengths and angles between its faces, making it one of the most symmetrical shapes in three-dimensional space. In this short tutorial video, I am modeling and unrolling an icosahedron. I studied […]

Modeling a rhombicosidodecahedron requires exploding and extending the faces of a dodecahedron and an icosahedron of the same edge length. We begin with both polyhedra centered at the same point. Then, we explode the faces of the dodecahedron and icosahedron outward from the center. We extend their planes while maintaining their orientation and shape. As these faces extend, they intersect and form new polygonal regions. Triangular and pentagonal faces emerge […]

I have come across several high school topics I was afraid of. While I was searching for a geodesic dome definition in Grasshopper, it was quite surprising that I found an easier way of modeling an approximation of icosahedron, the famous platonic solid. Icosahedron was a research topic of this website at various posts before (here, here, and here). In order to generate geodesic spheres, first I had to solve […]

Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

I tried different approaches to drawing platonic solids using Grasshopper’s native components. However, it seems impossible now. In geometric definition, a platonic solid is a set of points, distributed on a sphere with equal distances. If the set contains 12 points, then it’s an icosahedron. I found lots of information about these objects and mathematicians seem to love analyzing them. They created different approaches to building an icosahedron. One of […]

The dodecahedron is a Platonic Solid with 12 equilateral pentagonal faces. It has a close relationship with its 20-sided dual, Icosahedron. Mete Tüneri showed the following method of Dodecahedron construction, using only distances, corners of the pentagon, and a visionary equilateral triangle underneath. We’ll construct Dodecahedron, assuming that we’ve drawn an initial equilateral pentagon. We need to find out the pentagon’s angle of 3d rotation. First, put spheres at points a […]

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

Today’s polyhedra is the beautiful icosahedron. It is one of the five Platonic Solids with twenty equilateral triangular faces. Its dual is the dodecahedron, which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You […]