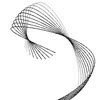
In this exercise, Grasshopper draws various Archimedean spirals. It constructs polar points and maps them onto a range of angles and a number of points. The spiral’s turning speed is determined by the constant “a,” while the constant “n” gives unique names to the spirals by raising the angle variable to the power of 1/n. Wolfram Mathworld names the spiral with n = -2 as lituus, n = -1 as […]
Posts with the keyword hyperbolic
We can create tessellations of outer points in a Poincare Disk, using the manual method explained in the last post (here). But repeating that compass and straightedge process is becoming a little useless after a couple of repeats. If you say “ok. I understood the concept, let’s get faster!” then we can model just the same process in Grasshopper3D to examine varying results in seconds; If we connect any grid of […]
The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear […]
Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here. Here is the Grasshopper3D file containing the above […]
[GHX: 0.8.0066] This is my second attempt on getting into non-euclidean representations of space. Althouth it seems easy at first sight, this represents a close point of theory between mathematics and contemporary computational design geometry. As always, architects tend to use mathematical terms such as “non-euclidean geometries” but as far as I saw, most of them have no idea about what it is. So, I’m trying to learn and understand this […]
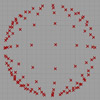
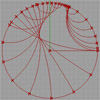
This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made […]