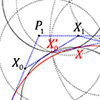
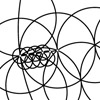
This is a new paper published in Nexus Network Journal. I tried to implement euclidean constructions by compass in the approximation of famous parametric curves; Bézier curves, and B-Splines. Then, I created the algorithms to calculate the number of steps on a compass-only construction of Bézier curves. I developed a simple Python script to simulate the geometric constructions. However, I have been studying this topic for nearly four years. In […]

This video shows the method of constructing equal segments on a line by only using compass operations. Here, you can see that there is a pattern in the number of required compass operations. For example, if you need to divide the distance by 3, you need 13 circles (or compass operations). This reveals a simple equation of c = 2 * n + 3 where n is the desired number […]

I learned this method from the open math resources website. I couldn’t help myself repeat it in Rhinoceros. It was quite fun to solve circle tangency problems in 2D, this is one of them: drawing the circle that passes three given points, not using ready-made commands but only geometric tools of the circle (compass) and ruler (line). Here is the sequence of it: First of all, we need to know […]

Here is a simple explanation of the famous Euclidean Constructions: Why didn’t Euclid just measure things with a ruler and calculate lengths? For example, one of the basic constructions is bisecting a line (dividing it into two equal parts). Why not just measure it with a ruler and divide by two?One theory is the the Greeks could not easily do arithmetic. They had only whole numbers, no zero, and no […]

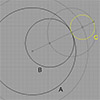
The first-year Architectural Geometry course includes Euclidean constructions as a study of associative geometry. We have exercised the below questions to study this topic. These are three mutually tangent circles, that can be drawn using only a compass and ruler, without built-in tangency functions in Rhino. Such exercises are expected to improve students’ reasoning. We believe architectural geometry education should encourage a conception that allows students to think about what […]

An octahedron is a polyhedron and platonic solid with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to […]

The dodecahedron is a Platonic Solid with 12 equilateral pentagonal faces. It has a close relationship with its 20-sided dual, Icosahedron. Mete Tüneri showed the following method of Dodecahedron construction, using only distances, corners of the pentagon, and a visionary equilateral triangle underneath. We’ll construct Dodecahedron, assuming that we’ve drawn an initial equilateral pentagon. We need to find out the pentagon’s angle of 3d rotation. First, put spheres at points a […]

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

A truncated Tetrahedron is an Archimedian Solid, created by slicing a Tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a Tetrahedron, first join its faces to create a polysurface. Now, you may re-create the lines of Tetrahedron’s edges, either by drawing them or generating them (Curve/Curve from Objects/Duplicate Edge). While the edge lines are selected, hit (Curve/Point Object/Divide Curve By/Number of Segments) and type 3 to create the […]

The tetrahedron is a platonic solid with 4 equal triangular faces (which are also equilateral), 6 equal edges, and 4 vertices. While creating this shape, we will take a closer look at length transfers using compass-like tools both in two and three-dimensional space. In order to define the edge length of the first triangle (which is a straight line), start with any two points in cartesian space. Using a compass […]