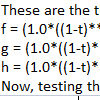This is the continuation of the previous post on parametric curve equations. In this new version, the script picks a NURBS curve from the user. Then, it analyses the curve’s degree and control points. Unfortunately, only the curves with degree+1 number of control points can be processed. In the future, I hope that I will be able to extend this script to include multi-span curves with more than degree +1 […]

The parametric curve equations are good examples to demonstrate the bridge between computer-aided design and mathematics. Although useless and pointless, it is a good exercise to extract the curve equations. In this Rhino Python code, I present a generalized equation extractor for Rhino. Rhino curves are good examples de Casteljau and Bézier curves. You can see the mathematical underpinnings of Rhino curves with this exercise: This code asks the user […]

Previous studies on trigonometric surface equations showed me an interesting alternative. This is the modification of the breaststroke surface definition. This time, I’m trying to fix the equation and change input values in a fashion that the waves of the surface are not symmetrical. Here are a few experiments on it; (Size, 44.8, X=10, Y=5, animating X’s from 0 to 32) (Size: 42, X=7, Y=5, animating X’s from 0 to […]

This was before Spherical Fantasies, while I was trying to update my surface equation definition. In between designerly intentions and mathematical facts, it’s hard to maintain a process, while keeping the definition yet simple and open to exploration. Grasshopper definition is here: [GHX: 0.8.0066] A little tired of mathematical definitions, I started to give names to the animate surfaces I develop. Like the Spherical one, this is also a trigonometric equation […]

This is about conforming distortions on surfaces and creating imperfect (say ugly) surfaces. I started with planar surfaces, however, I continued with spherical ones. There are interesting results when applying trigonometric functions to spherical surfaces. Example surface equations: W=(sin(x*y)) / 2 and W=(cos(x)+sin(x-y²)) / 2 Please be patient if animations are loading slowly. But they represent a way of creating free-form-looking surfaces, highly mathematical behind the scene. Here is the […]

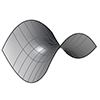
This is another popular “math surface” being rediscovered by designers nowadays, in 2012. Saddle surfaces, seen above as mentioned earlier (here) have a special type named “Monkey Saddle Surface”. This surface was a dramatic example of how Grasshopper can control equations and instantly show graphical results. The mathematical equations start with Z=… this makes it very easy for us to transform any x-y grid centers (a 2d data tree of […]