The Möbius strip is a famous mathematical object. Although being in three-dimensional space, it is a closed-loop of only one surface and only one edge. This quality alone makes the object an interesting study for computational design. I aimed to create an object to test our new CNC machine. I wanted to test the egg-crate interlocking fabrication method. This is why the study became a Möbius strip fabrication. Apart from […]

A previous work showed a method to create interlocking structures to be created without boolean operations. This time, a small addition is made to create waffle objects using two surfaces, one is the top surface, and the other is the bottom. It was a small modification at the beginning; to replace the “extrude” component with an “edge surface” component. But the interlocking details are now different at each intersection, so […]

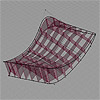
This is a basic formation of component-based design in a dataflow environment. A double-curved surface is subdivided and re-constructed using straight sections. Parametric model of a surface construction by variable components. The main data list of subsurfaces are distributed into four distinct lists, that will be used to construct lines out of double-curved quadrilateral faces. Such definitions could be further advanced by adding a precise fabrication detail. Parametric definition can […]

It has been a tough problem for me, for the last two days. A parametric model of an interlocking structure (sometimes also called egg-crate, waffle, or contouring structure) can be created easily in Grasshopper using a Contour component. In addition, you need a couple of list management operations and a boolean (or region) difference event. However, Rhino and Grasshopper are very slow at calculating boolean differences on both solids and […]

NURBS surfaces by nature, like four-corner topologies with U and V directions. Şebnem Yalınay Çinici has formulated a tectonic exercise of “Primitive Hut”, which in my point of view is a tough geometric challenge; a subdivision on a real three-corner manifold. That seems very easy at the beginning as both Rhinoceros and Grasshopper are able to create surfaces with three corners, by either lofting, meshing, or edge curve methods. However, those […]