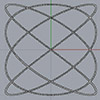
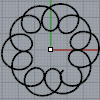
Today’s beautiful curve is the spherical cycloid. It is a cycloid, rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting than the regular planar cycloids, epicycloids, and hypocycloids. This curve is believed to have been studied first by Jean Bernoulli in 1732. The interesting and […]
Posts with the keyword cycloid
This RhinoPython script handles the simple graphs of two-dimensional parametric functions. Therefore, it approximates these functions by drawing parametric curves. It generates many points by solving the functions. The graph of parametric functions is a major topic in most Design Mathematics courses. Because it looks like the building block of many concepts of CAD. However, there is much more to learn before saying that the third degree NURBS is a […]
Studied earlier in Grasshopper here, creating a cycloid-like curve actually mimics the physical process of rotating disks on a path. Below is a test in Rhino Python. # Drawing Cycloid-like Curves # 07.08.2017 www.designcoding.net – Tugrul Yazar import rhinoscriptsyntax as rs curv = rs.GetObject(“Select curve”) qual = rs.GetInteger(“Quality”,100) radi = rs.GetReal(“a radius”,4) radi2 = rs.GetReal(“Circle radius”,4) cua = rs.OffsetCurve(curv,[1,1,0],radi2) cevre = 2 * 3.1415 * radi mimi = [] for […]
This is a Cycloid-like family of curves, generated by its classical description: a rolling circle. I had several other studies on similar topics before. In this cycloid experiment, I used Grasshopper in which, we don’t need to roll the circle. Instead, we can divide a parametric curve, utilizing data lists to simply rotate a circle around it. Finally, evaluating the circle repeatedly creates a Cycloid-like result. I found this as […]