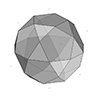
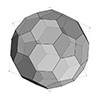
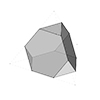
In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron, or omnitruncated icosahedron is an Archimedean solid. It is one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces. In this short tutorial, I am constructing an irregular truncated icosidodecahedron. It is not the regular Archimedean solid, but a rough approximation of it. I made this model to exercise the exploration of […]

The rhombicosidodecahedron, an Archimedean solid, is one of the 13 convex polyhedra made up of regular polygons. While all its faces are congruent, they consist of various types of regular polygons. I previously explored this fascinating polyhedron and am revisiting it now as part of the Architectural Geometry course. In this short tutorial video, I demonstrate the modeling of a rhombicosidodecahedron. Despite its lengthy and unusual name, this polyhedron is […]

A truncated cuboctahedron is an Archimedean solid, meaning it is a highly symmetrical, convex polyhedron with identical vertices and faces of regular polygons. As its name suggests, you can create the truncated cuboctahedron by truncating (cutting off) the vertices of a cuboctahedron. A cuboctahedron is a rectified cube. After you model it, you can divide all its edges into 1/3s. Then, connect those division points to draw the squares, hexagons, […]

An icosidodecahedron is a polyhedron that is part of the family of Archimedean solids. It has 32 faces, consisting of 12 regular pentagonal faces of a dodecahedron and 20 regular triangular faces of an icosahedron. It is highly symmetrical, with the same arrangement of faces around each vertex. In this short tutorial video, I am modeling and unrolling an icosidodecahedron. This polyhedron is very interesting and is mostly used as […]

The truncated octahedron is an Archimedean solid, characterized by a mix of hexagonal and square faces, and it has a very symmetrical and regular structure. Buckminster Fuller called this solid “Mecon”. The truncation process includes the cutting the edges of a polyhedron. We do this by dividing every edge of the polyhedron into 1/3s. Then, we carefully re-connect these division points to generate new, planar polygons. In the case of […]

Buckminster Fuller used the term “dymaxion” for a variety of his designs, and one of these was the dymaxion map. It was based on the geometry of a polyhedron. While the dymaxion map is more directly related to the icosahedron, Fuller’s work often involved using other polyhedral shapes. One of them is the cuboctahedron. He used this term for various conceptual and practical designs, particularly in the context of his […]

A Buckyball, (or Fullerene), is a molecule of 60 carbon atoms with a structure resembling a soccer ball. It is a specific type of fullerene, often referred to as C60, where the carbon atoms form a series of pentagons and hexagons in a pattern that creates a spherical shape. This structure is similar to the arrangement found in a truncated icosahedron, with 12 pentagonal and 20 hexagonal faces. The buckyball […]

Truncation in mathematics and geometry refers to cutting off parts of a shape, typically the vertices, edges, or other extremities, to create a new modified figure. This process is often used with polygons, polyhedra, or functions. A truncated tetrahedron is a polyhedron we can derive from a regular tetrahedron by truncating (cutting off) its four vertices. This process creates a new shape with additional faces while maintaining its symmetry. In […]

Today’s polyhedra are the famous Archimedean Solids! I created a simple Grasshopper script to generate pendants from these beautiful solids. I call this Archimedean Pendants. However, you can implement other polyhedra to the same code. I hardcoded the vertex coordinates so you won’t need an extra add-on to generate the polyhedra. Thanks to the new SubD component Multipipe, it makes life much easier to produce 3dprint-ready results. To make this […]

An Archimedean solid is a convex isogonal (vertex-transitive) and nonprismatic solid that is composed of two or more regular polygonal faces. There are thirteen such solids in geometry. Coding the snub dodecahedron study aims to generate one of these solids, composed of 12 regular pentagons, and 80 regular triangles. You can generate the snub dodecahedron by expanding and twisting the faces of a dodecahedron outward. This also creates rhombicosidodecahedron, which […]

Stellated polyhedra are three-dimensional geometric shapes formed by extending the faces of a regular polyhedron (a solid with flat faces) beyond their original boundaries until they intersect with each other. The term “stellate” comes from the Latin word “stella,” meaning star and these polyhedra often have a star-like appearance due to their extended faces. They are popular because of their aesthetic qualities. I studied these forms many times before. This […]

Archimedean Solids are convex polyhedra with faces of regular polygons and vertex-transitive. There are 13 such objects (excluding prisms and antiprisms which are probably less exciting). In this study, I experimented with these solids and designed a family of planters. Since they are convex and look cool, I decided to give it a try. I call this algorithm Archimedean Planters. The first part of the definition deals with the generation […]

While digging through the lecture archive, I found this video I made in 2017. We introduce Platonic solids and Archimedean solids in the Design Geometry course at Istanbul Bilgi University. This video shows how we can create an Archimedean solid, the Truncated Tetrahedron, by folding it from a flat sheet.While doing this, I intersected the spheres by using the relations between the side lengths of the solid, and I calculated […]

Lokma is the name of a pastry made of fried dough soaked in sugar syrup or honey and cinnamon, typically shaped into a ring or ball. Unfortunately, it is not the “Lokma” we’ll study here. In Turkish, there is another meaning of the same word related to the history of Eastern architecture. It is the name of metal connectors in railings, mostly inside of the openings of garden walls and […]

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

A truncated Tetrahedron is an Archimedian Solid, created by slicing a Tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a Tetrahedron, first join its faces to create a polysurface. Now, you may re-create the lines of Tetrahedron’s edges, either by drawing them or generating them (Curve/Curve from Objects/Duplicate Edge). While the edge lines are selected, hit (Curve/Point Object/Divide Curve By/Number of Segments) and type 3 to create the […]