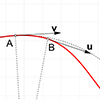
Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a tangent circle that has the same curvature as the curve at point P. The larger the circle, the more “flat” the curve is. An infinitely […]
Another famous shape of architectural geometry is a set of definitions creating minimal surfaces. I’ve found the trigonometric equation of the Gyroid and created a simple logic for approximating it as points in Grasshopper. However, when I searched the net for similar solutions, I found lots of them including the same approach as mine (Wynstan Wu’s definition). I was planning to develop a script in Grasshopper to take these estimated […]
