This week’s fractal is the famous Dragon Curve. Dragon Curve exhibits self-similarity, meaning parts of the curve resemble the overall shape, regardless of scale. It’s fascinating because a relatively simple construction process generates a complex and visually captivating fractal pattern. The Dragon Curve is often used to demonstrate fractal properties in mathematics and is popular in recreational mathematics due to its intricate and beautiful patterns. It has applications in computer […]
Posts with the keyword anemone
In this study, I explore Cesaro Fractal, generated by Grasshopper. Usually, it is not possible to code recursive algorithms in Grasshopper. With the help of the Anemone add-on, these fractal curves are easy to model. I studied similar fractal algorithms here before. This one is very similar to the Koch’s snowflake. The only difference (as far as I understood) is the side of the spikes. Koch’s Snowflake generates triangular spikes […]
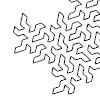
Anemone components are still working great, extending the abilities of Grasshopper. Here, I studied a space-filling (or plane-filling) fractal called the Gosper-Peano Curve. You should be very careful about the number of iterations (the N input). Because it can crash your Rhino if you change it to more significant numbers. Also, you should have Anemone components installed in order to run this definition. The generator curve is a special one. […]
I’ve been searching for a way to implement edge bundling on Grasshopper. It is an effective visualization technique that you can use in connectivity diagrams. There are a couple of different approaches to this problem. It is a nice way to analyze common paths within crowded graphs. I’ve found several entries in the Grasshopper blog about this subject, but only implementing Kangaroo seemed to be a complete solution. My approach […]