Sunflower Spiral

by Tuğrul Yazar | December 22, 2011 00:09

Sunflower Spiral (or Phyllotaxis[1]) can be constructed in Grasshopper according to Vogel’s model of parametric relationships. This model uses polar coordinates. You can download the Grasshopper definition file here:

(The Grasshopper file is still working after more than 11 years -15.12.2022. This is such a powerful quality of Grasshopper, I think.)

It’s a good example of utilizing polar coordinates. It’s also fun to play with the parameters and constraints of the Sunflower Spiral. Also, there are very interesting results if you also connect the polar angle value to the “z” of the point component.

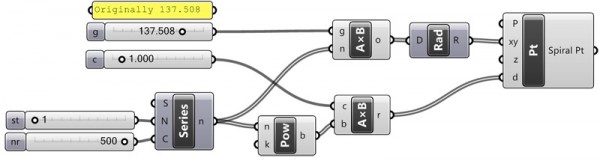[3]

According to Science.org[4]:

Mathematical biologists love sunflowers. The giant flowers are one of the most obvious—as well as the prettiest—demonstrations of a hidden mathematical rule shaping the patterns of life: the Fibonacci sequence, a set in which each number is the sum of the previous two (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …), found in everything from pineapples to pine cones. In this case, the telltale sign is the number of different seed spirals on the sunflower’s face.

Count the clockwise and counterclockwise spirals that reach the outer edge, and you’ll usually find a pair of numbers from the sequence: 34 and 55, or 55 and 89, or—with very large sunflowers—89 and 144. Although the math may be beautiful, plant biologists have not worked out a mechanistic model. Thus, this fully explains how the sunflower seed patterns arise. The problem is that plants don’t always show perfect Fibonacci numbers.

Source URL: https://www.designcoding.net/sunflower-spiral/

---