NURBS surfaces by nature, like four-corner topologies with U and V directions. Şebnem Yalınay Çinici has formulated a tectonic exercise of “Primitive Hut”, which in my point of view is a tough geometric challenge; a subdivision on a real three-corner manifold. That seems very easy at the beginning as both Rhinoceros and Grasshopper are able to create surfaces with three corners, by either lofting, meshing, or edge curve methods. However, those surfaces, then cannot be used to develop sub-surfaces because of the need to define U and V directions. Then, Rhino seems to add an extra invisible corner and get the shape triangular by actually forcing a cut on a four-corner surface.

In my case here, that seems to be solved by trimmed surfaces. A four-corner surface is split across to create two triangular surfaces. The definition of the cutting path was the first challenge in Grasshopper3D. You may download the file and check here [2011_12_12_hut].

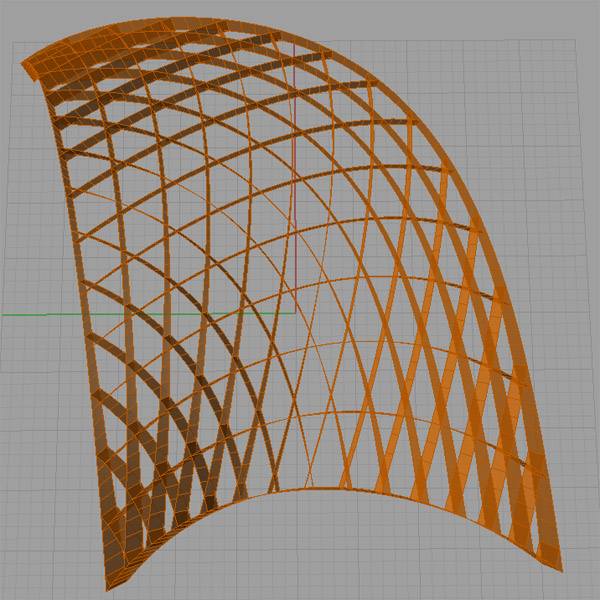
After that, the proposed design solution was to create an egg-crate structure that has three axes of offset curves. As there seems to be a problem with Grasshopper3D, it cannot run offset on the surface properly in every condition. So, I decided to create those sections also using surface UV parameters. That was a nice list management exercise because the lists of UV indexes change sequentially in every row in every direction. In order to develop variations, I decided to experiment with some sort of curve selection using patterns, which may be different in all three directions. You’ll see that in the definition file also. If you put the same pattern in every direction, the output is composed as shown above. Different pattern inputs create various solutions such as shown below;

In order to model the solid sections, each curve is extruded in a rule, that as high as it reaches, the sections are becoming thinner. Typically, egg-crate structures use planar contouring, which fails when the base surface “tumbles”. In this case, I used surface normals to calculate thickness, so it’s still stable in even harder double-curved surfaces. Of course, the material used to physically construct this system should be able to bend and twist (cardboard for example).

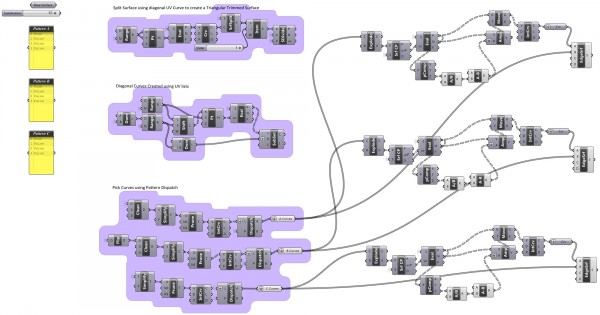
There are some parameters left for the exploration of different variations. The result seems to be a solid and stable solution to most problems of egg-crate structures which has three corners. Further studies may include adding labels and CNC cutting-friendly outputs.