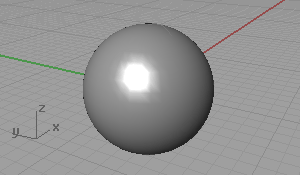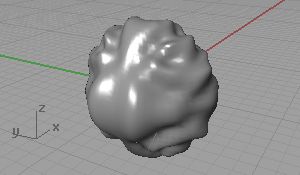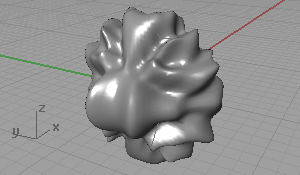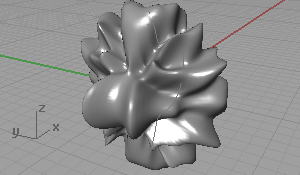
This is about conforming distortions on surfaces and creating imperfect (say ugly) surfaces. I started with planar surfaces, however, I continued with spherical ones. There are interesting results when applying trigonometric functions to spherical surfaces. Example surface equations: W=(sin(x*y)) / 2 and W=(cos(x)+sin(x-y²)) / 2

Please be patient if animations are loading slowly. But they represent a way of creating free-form-looking surfaces, highly mathematical behind the scene.

Here is the Grasshopper definition: [GHX: 0.8.0066]

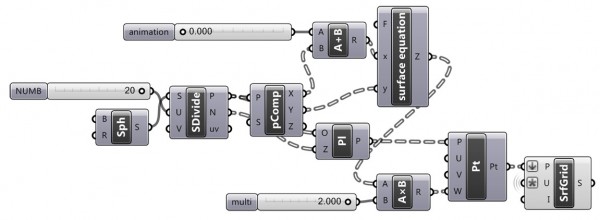
As you see, I used the UVW coordinate system of the sphere, subdivided into 20 pieces. W represents the amount of distortion from the ideal sphere.