Spherical Cycloid

by Tuğrul Yazar | April 2, 2024 19:39

Today’s beautiful curve[1] is the spherical cycloid. It is a cycloid[2], rolling on a 3d circular path rather than a straight and 2d one. There are algebraic explanations of this curve. Therefore, I find it interesting to experiment with them, since it is more interesting than the regular planar cycloids, epicycloids, and hypocycloids. This curve is believed to have been studied first by Jean Bernoulli in 1732. The interesting and playful part of this is the resulting curve is always on a spherical surface. I prepared two Grasshopper Python[3] scripts for this study. The first one generates the x,y, and z coordinates of spherical cycloid variations. So, you can connect them to points and curves. The second script calculates the center and radius of the sphere the curve is on.

This Grasshopper definition generates variations of spherical cycloids and their spheres. It is an educational and exploratory code to learn Grasshopper and generate interesting designs with it. The inputs of the definition control the a, w, and b parameters of the formula and the t domain. The output of the code is the ordered list of x, y, and z values of the points on a spherical cycloid. Therefore, it is ready for further investigation and modeling. Another script inside the code calculates the height (z) and radius of the sphere. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work.

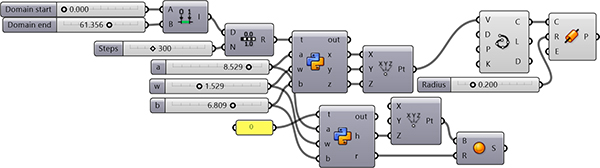
You can rebuild the definition by looking at the diagram above. However, there are two Python components. I took the parametric curve formulas inside these scripts from the Mathcurve website. However, if you want to download my Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[4] including the Grasshopper files for the Spherical Cycloid and more. 

Source URL: https://www.designcoding.net/spherical-cycloid/

---