Spatial Mapping made Easy

by Tuğrul Yazar | April 19, 2012 13:53

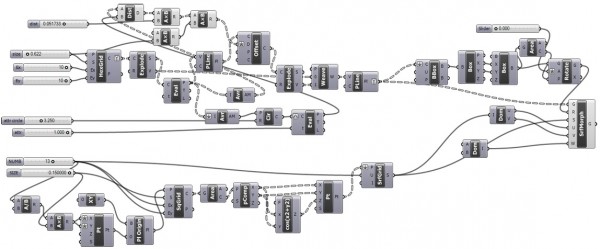
Trying to further improve my experience in parametric modeling, I’m mixing and joining old definitions to reveal different potentials. I’m experiencing spatial mapping or morphing in Grasshopper. This is an equivalent form of the “flow along surface” command in Rhinoceros. It re-builds a geometric composition over another space (from world XY coordinates onto a surface with UV coordinates here) This is especially useful in creating surface compositions from famous tessellations such as Voronoi. There are lots of things I can do with this functionality. Here is the first example of reconstructing the previous work of Islamic patterns (here) onto a parametric surface (described here). My first definition is here [GHX: 0.8.0066]. This saves me lots of time; a non-uniform parquet deformation is projected onto the space of the surface with equation cos(x2+y2). There is a point attractor on the reference pattern that travels on a planar circle. However, not itself, but the “ghost” of that point is also projected on the surface.

The second animation (on the right) rotates the bounding box so that curves are rotated-projected. The third animation (below) is the study of surface coordinates that no longer uses the surface itself, but rather incorporates with the manifold, the abstract space it represents. It simply scales the bounds of the surface equation. This is somehow both terrifying and beautiful, how a constant increase of a slider parameter creates those movements on the surface. (Be patient if the animation loads slowly) Again, I fell in love with mathematics.

[1]

Source URL: https://www.designcoding.net/spatial-mapping-made-easy/

---