Space-filling Elongated Dodecahedra
by Tuğrul Yazar | February 22, 2024 19:25
The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of the dodecahedron but is stretched out. The elongated dodecahedron might not catch your eye at first—it’s just a long version of a shape you’ve probably seen before, and it seems pretty basic. But don’t be fooled by its simple appearance! This shape is secretly a genius when it comes to filling up space without any gaps or overlaps. I developed this Space-filling Elongated Dodecahedra structure in Grasshopper by utilizing the vertex coordinates of the polyhedron. Then, I defined three vectors to copy it in three directions. You can cut the output of the code and analyze the interior spaces, as seen in the animation.
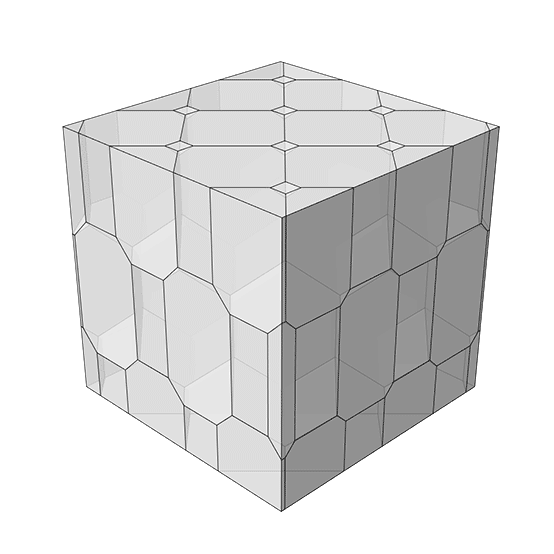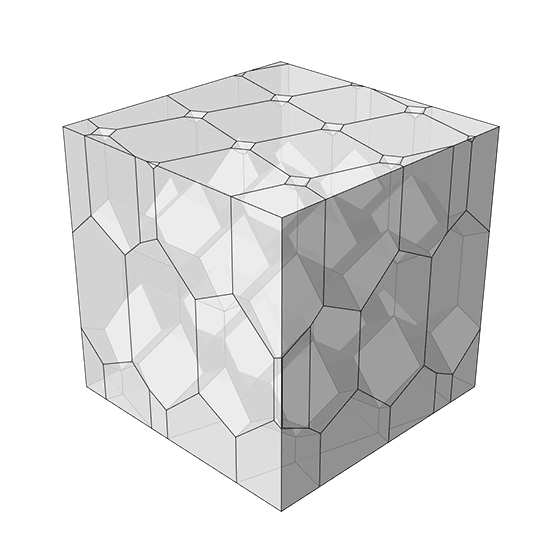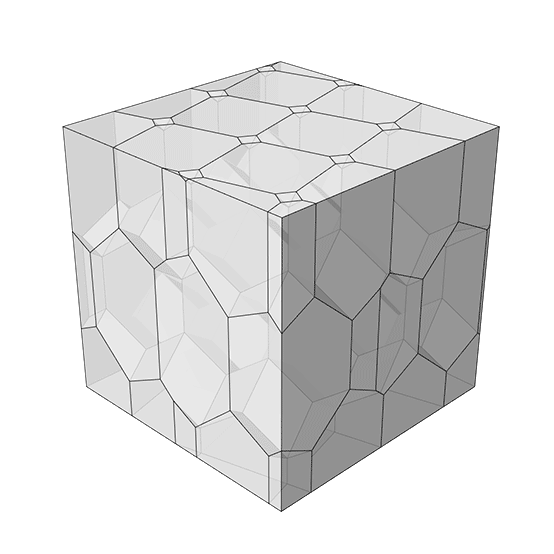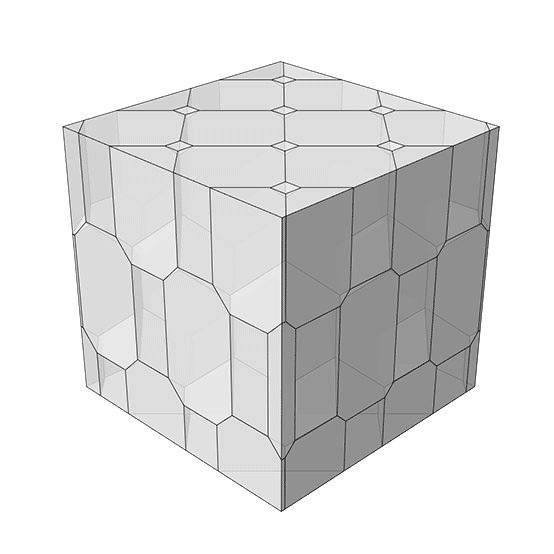
This Grasshopper definition generates the Space-filling Elongated Dodecahedron structure. The input parameters are the number of cells in three directions. The output of the definition is the solid 3d model. It has a structure with individual cells. Therefore, it is ready for 3d printing. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work.
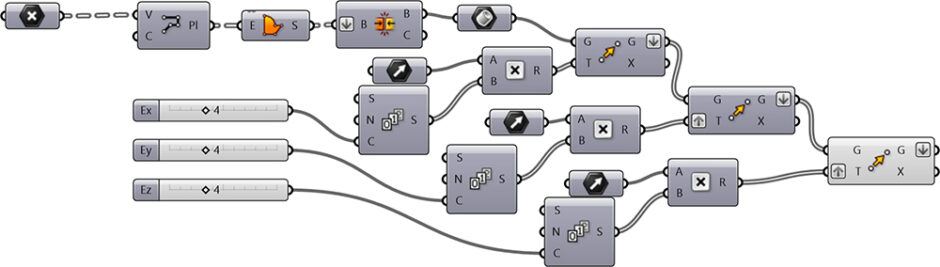 [1]
[1]You can rebuild the definition by looking at the definition above. However, you will need the vertex coordinates of the Elongated Dodecahedron. You can check the Parakeet add-on to get them probably. However, would you consider being my Patreon if you want to support this website and download my Grasshopper file? Here is the link[2] to my Patreon page, including the Space-filling Elongated Dodecahedra and more. Thank you.

- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2024/02/Space-filling-Elongated-Dodecahedron-def.jpg
- Here is the link: https://www.patreon.com/posts/space-filling-99002718?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
Source URL: https://www.designcoding.net/space-filling-elongated-dodecahedra/