Snub Square Tiling

by Tuğrul Yazar | October 22, 2012 14:45

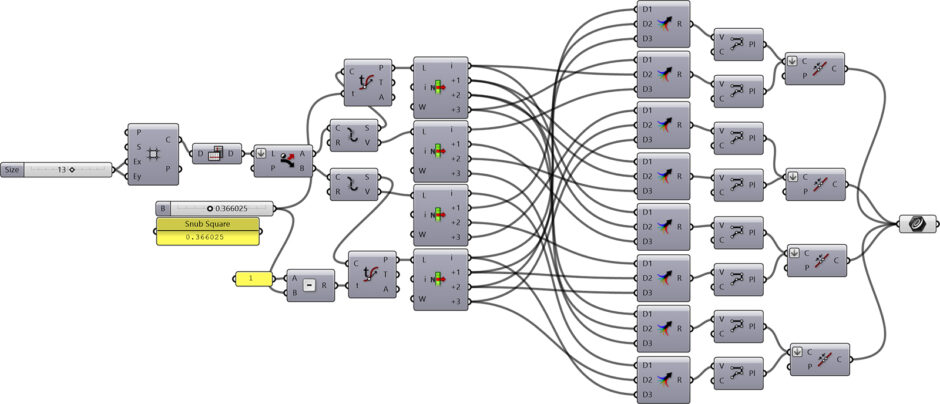
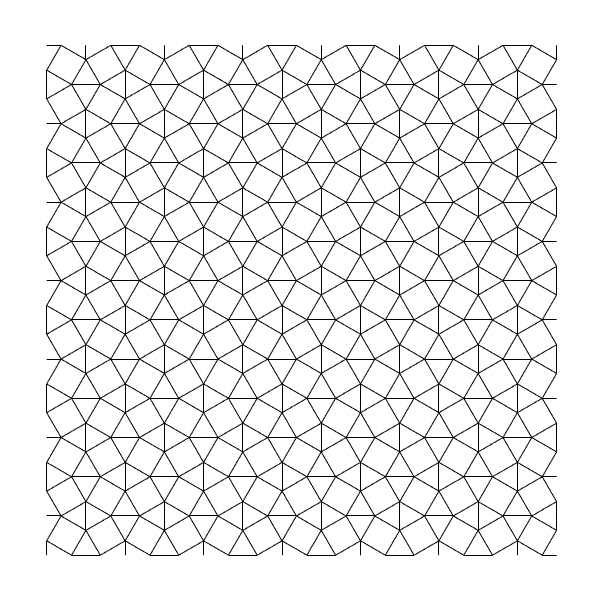
Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling[1] I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral triangle. Now, we have a snub square tiling, composed of tilted squares, but to process it further and explore different potentials, I had to tell Grasshopper about the equal triangles also. So that made the definition a little bit more crowded because I had to connect proper vertex IDs of different grid cells and join them together to emerge new shapes:

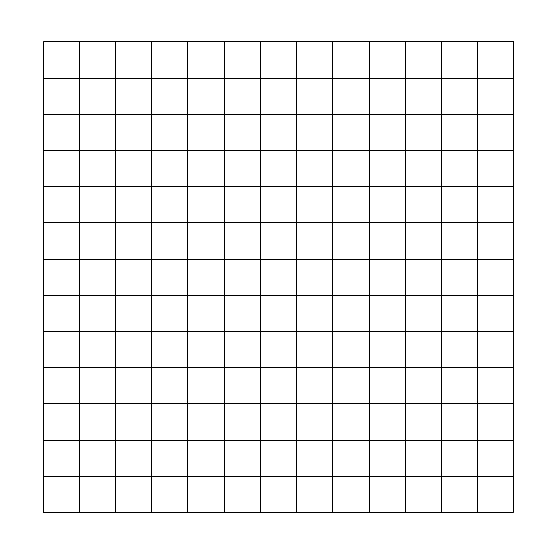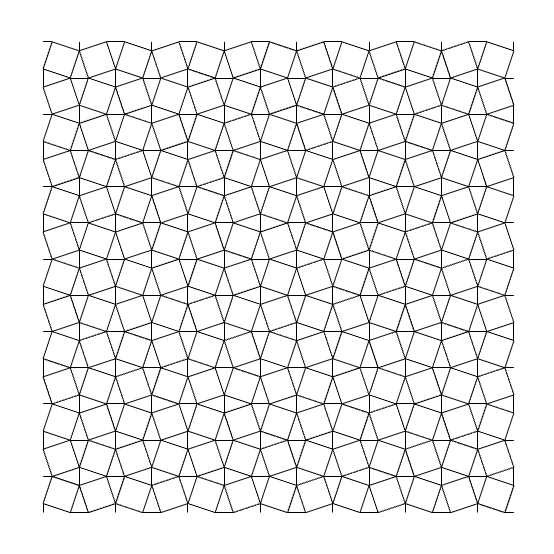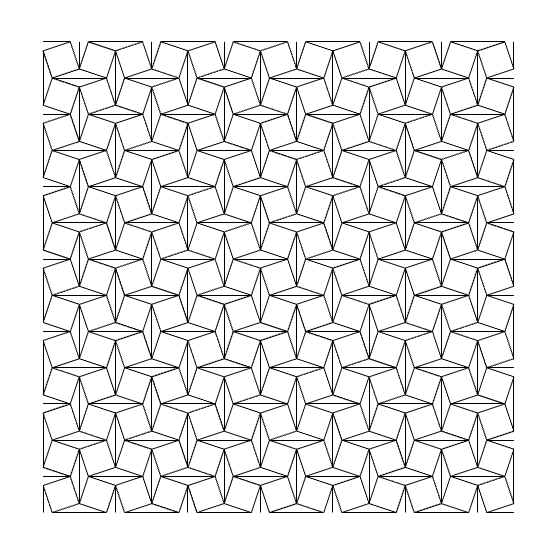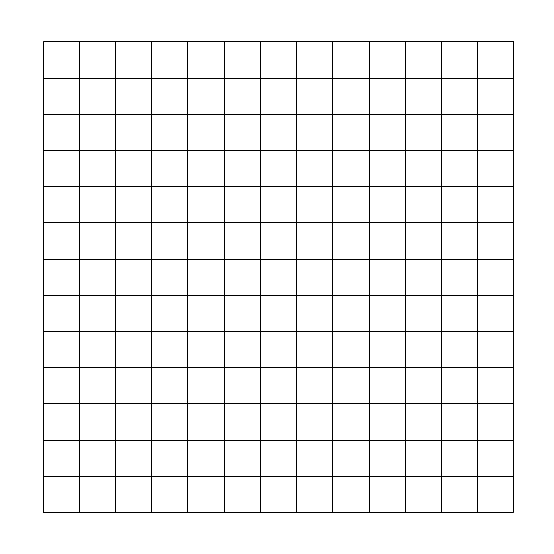
Then, I played with these vertices to produce the following results. Note that you can map these definitions onto any surface as we did before. This set of Grasshopper definitions re-generates the Snub Square Tiling along with its variations. The inputs are the x and y sizes of the lattice (grid). The output of the definitions are sets of lines of the tessellations. You can reverse-engineer these definitions and learn a lot about the geometric constructions. The output is ready for further investigation and development.

You can rebuild the Grasshopper definitions by checking the diagrams on this page. I used native Grasshopper components while developing this design. Thus, you don’t need any add-on to run it. However, if you like my content and want to support me, would you consider being one of my Patreons? Here[3] is the link to my Patreon page, including my working Grasshopper files for Snub Square Tiling and more.

Source URL: https://www.designcoding.net/snub-square-tiling/

---