Snub Square Surface

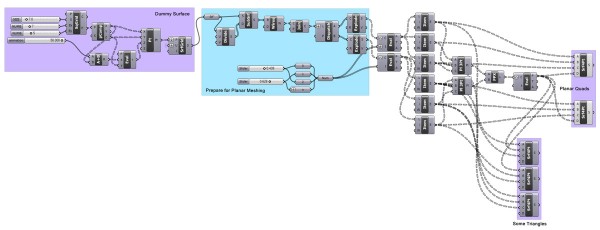
For the last 10 days, I’ve been searching for a proper algorithm for representing surfaces using planar shapes. It is obvious that triangulation is an answer but there is an interesting research topic of planar remeshing using shapes other than quads, hexagons, or any other regular polygons. Especially in computer graphics, such things refer to the optimization of models to decrease the load of GPUs. In the Grasshopper community, this has also been discussed and there is a great implementation at the Trada pavilion by Ramboll Computational Design Team (link here). There are some professional planar remeshing algorithms out there also such as TPI (Tangent Plane Intersection). I tried to implement various approaches and hopefully will present some results shortly.

By that time, I tested a quick solution; just confirming a two-dimensional tessellation onto the given surface, then manipulating the cells in order to achieve partial planarity. The first test was using the famous snub square tessellation (discussed here). I thought it would be interesting to implement snub square tessellation on a surface, (of course, squares would be bent); then move one vertex of each cell to make those squares planar. There is also another test (here) in this blog that can be regarded as the starting point of this.

However, in snub square tessellation, there is a more sophisticated problem of squares sharing corner vertices. Those vertices should be moved to meet both squares’ planarity at the same time. This is why I used plane intersection to find a point that meets both conditions.

After adding parameters to curve evaluation, I realized that it is no longer a snub square tessellation, but it includes planar quads on a surface in a fashion that can be fabricated using 3-axis machining. The definition is a little bit messy. You can download and test it here: [GHX: 0.9.0014]