Today’s computational curve is the beautiful Sierpinski Triangle. It is a fractal named after the Polish mathematician Waclaw Sierpinski, who described it in 1915, though it had been previously described by other mathematicians. It is a self-replicating pattern that arises from a simple recursive process. To construct the fractal, you start with an equilateral triangle and then repeatedly remove smaller equilateral triangles from its interior, leaving holes. Each iteration involves dividing each triangle into four smaller triangles and removing the middle triangle. Then, you repeat this infinitely. The Sierpinski triangle exhibits self-similarity, meaning that it looks the same at any magnification or scale. It is a fascinating example of how simple rules can lead to complex and beautiful patterns in mathematics.

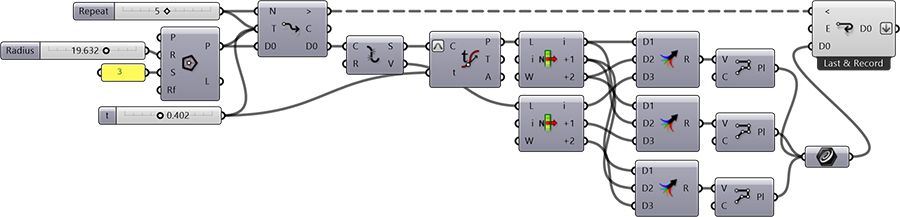
This Grasshopper definition generates the Sierpinski Triangle and its improvizations with several input parameters. The number of iterations, initial radius, thickness of the lattice, and evaluation parameters are the user-controlled inputs. So, you can generate the original Sierpinski Triangle and several deformed variations of them by playing with the inputs. The outputs are a planar surface and closed polylines of the resulting lattice. Therefore, it is ready to be laser-cut. I made the definition with the help of the Anemone iteration components. So, you need to install it to be able to use the definition.

You can rebuild the definition by looking at the diagram above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? The link to my Patreon page includes the working Grasshopper file for the Sierpinski Triangle and more.