Back in 2011, one of the first posts on designcoding explored how to divide a surface in alternative ways. I called this Grasshopper definition a semi-regular surface tessellation. Although the term isn’t entirely accurate -since the pattern is neither planar nor made of equilateral shapes- it still reflects what I had in mind. Dividing surfaces into fabricable parts remains a key concept in learning parametric modeling, so I decided to revisit and update this old definition. There must be many add-ons and methods to do that. This definition is rather a beginner’s guide. I internalized the NURBS surface into the definition. So, you can change it to apply the pattern on any Rhino surface.

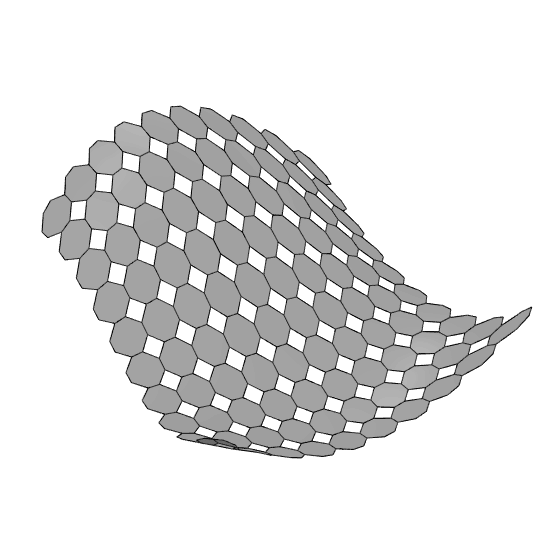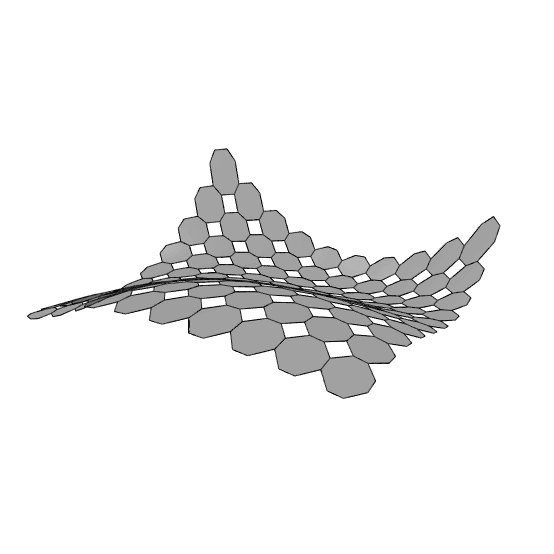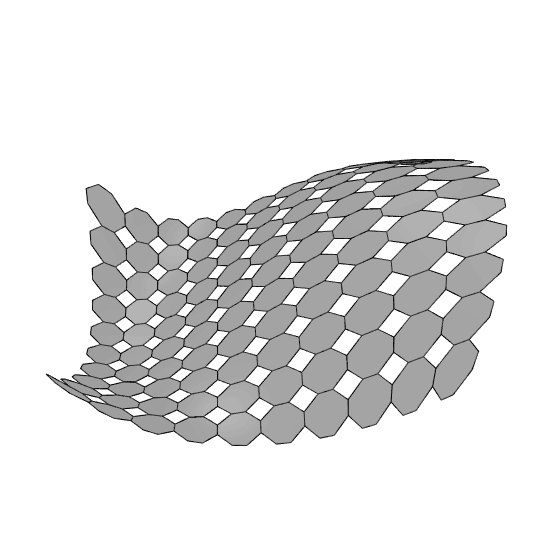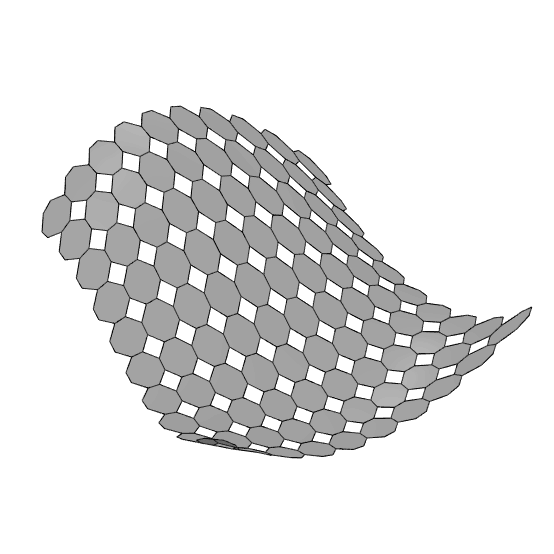
The process begins by dividing the surface into quadrilaterals along the U and V directions using Isotrim and Divide Surface. On each subdivided surface, I create a 3×3 grid with Isotrim. Then, I generate octagonal and quadrilateral tiles by selecting specific vertices from the grid. You can use more adaptive methods instead of fixed vertex indices; this approach is probably the simplest for this pattern. Interestingly, even after 14 years, Grasshopper’s handling of these components and their vertex numbering has remained the same.

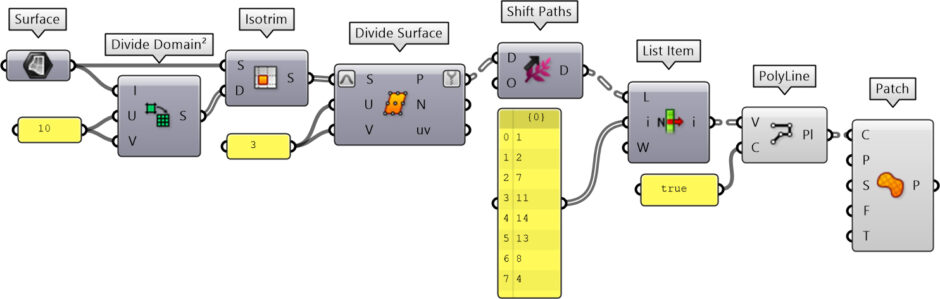
You can rebuild the definition of semi-regular surface tessellation by looking at the diagram above. However, if you want to support my website by downloading my working Grasshopper file, would you like to be one of my Patreons? The link to my Patreon page includes the Grasshopper file for semi-regular surface tessellation, and more. Thank you for your support.