Circle Packing Experiments

Since last week, I’m very curious about circle packing. There are a couple of complete solutions on the internet. I’m still in the early steps of such a solution yet. A full circle packing means that it does not include any gaps and each circle is tangent to all possible neighbors. Sounds easy in Grasshopper but I couldn’t see any solution yet. There are some circle-packing attempts but they have gaps. Also, I don’t want to use an evolutionary solver (Galapagos) or a physical engine (Kangaroo) because I believe there is a solid geometric solution other than an agent-based optimization. Anyway, I need complete packing, no pushing circles leaving gaps. Even, maybe I’m not searching for a solution, I’m searching for a method.

It might be much easier in a recursive scripting environment, but I believe there is a method to model a solution in dataflow, particularly in Grasshopper3D. So far, I established very early parts of the problem: The equations of a Doyle spiral, and K. Stephenson’s edge-angle equation of tangent circles.

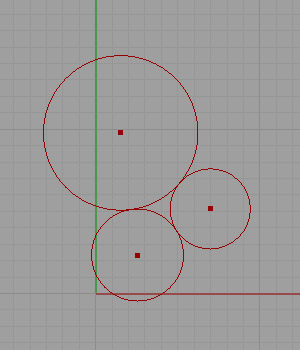
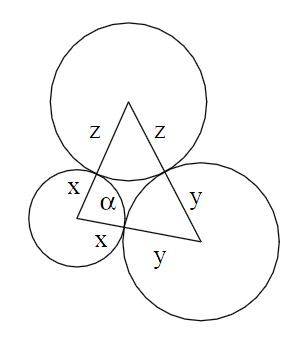
We used to take a “Circle tan tan” function and use it to create a circle that is tangent to two others easily and quickly. But there is a solid mathematical background to it. The angle alpha above can be computed with the:

*

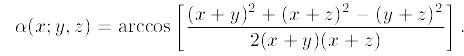which can be defined in Grasshopper:

This way, we can create three tangent circles just by entering their radii. The rest is math;

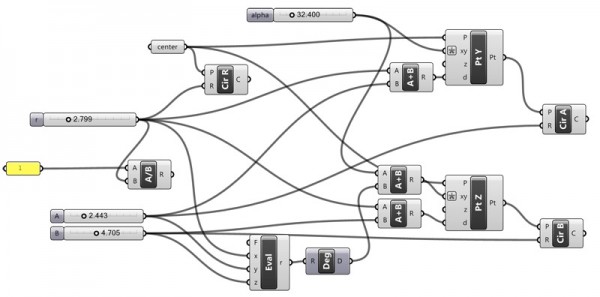
Here is my Grasshopper3D document: [GHX: 0.9.0006]

Then, I multiplied this process to create one flower of a Doyle spiral, a famous rule that explains the relationships of 6 tangent circles’ radii. This is really interesting;

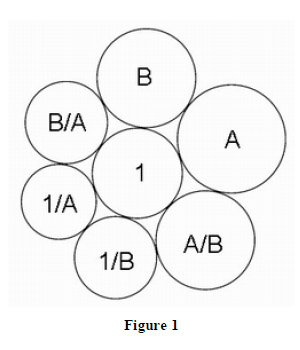
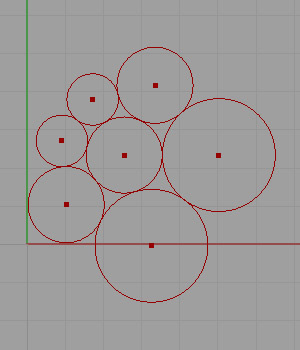
But it’s true! Peter Doyle was actually correct! I proved it. :) Here is my study document on this: [GHX: 0.9.0006]

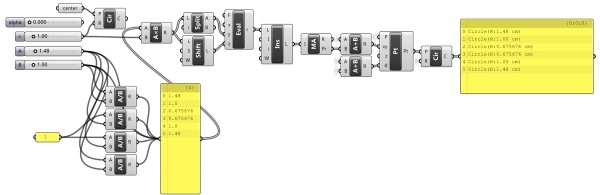
I’m still searching for it. I see the solution in a recursive process, Hoopsnake would be an answer, but first I’ll have to know that it is really impossible in native Grasshopper3D.

This website has a bibliography about circle packing. Also, google “Doyle Spiral” and you’ll find an interesting geometric research subject.

I would argue that CirclePack is to a geometer what a moderately well-equipped laboratory is to an organic chemist (only safer). The potential for open-ended experiments is unique, and yet the machinery is accessible to people at all levels; who knows, a few experiments and you or your students might be hooked!

Circle Packing: A Mathematical Tale, Kenneth Stephenson