Rhombille Tiling on Surface

by Tuğrul Yazar | June 13, 2023 10:23

This is an update on my 2012 exercise on rhombille tiling. This reminded me of the old-school subdivisions of surfaces again after 11 years. It was while reading about rhombic dodecahedron[1] (the stackable solid), that I came across this cute tiling. It’s quite simple, just a hexagonal grid with a special reconstruction. I decided to recreate it by using well-known native Grasshopper components. I animated the result with a variation of the Breaststroke surface function (described here). Then I reconstructed as three quadrangles with proper vertex IDs. These IDs are always the same. So it seems that it is possible to apply it to any Rhino surface.

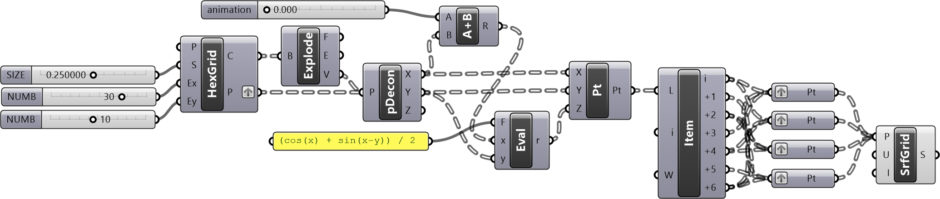
You may subdivide any surface to create such tessellations, this time I chose to rebuild the surface from hexagonal cells. In this Grasshopper definition, first, I developed the surface by using a function. This function gets x and y values and generates a z value. After creating the surface, I decompose and map a hexagonal grid onto that surface. One can simplify this definition better in the future. However, this works very well. It is also educational for beginners of Grasshopper. It looks like a paneling at first. But it is not, because there is no flat planarization here.

[2]

I updated the 2012 definition in 2023. I wrote the equation of the function in a Panel. You can rebuild the definition by looking at the definition above. However, the List Item indices are a bit tricky. Here are the index orders of those four Point containers: (0,3,6), (6,4,0), (1,2,4), and (2,6,5). But if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[3] including the working Grasshopper files for the Rhombille Tiling and more.

Source URL: https://www.designcoding.net/rhombille-tiling-on-surface/

---