Quadrilateral Surface Tessellation

by Tuğrul Yazar | April 9, 2012 01:16

As far as I understood, it is impossible to physically construct double-curved surfaces from quadrilateral and planar faces. This definition tries to find an optimized alternative to this problem. Any surface, single or double curved, is divided into standard sub surfaces. But this time, those surfaces are treated as planar surfaces, therefore one corner is moved to meet this requirement. The output consists of only planar surfaces ready for fabrication. Here is the initial definition [GHX: 0.8.0066]. There are potential improvements to this definition such as finding the best solution at each subsurface for minimum distortion from the original surface.

The above animation (left) uses Cos(Abs(x)-y) equation as a test surface with expansion in x and y directions. The one on the right is a monkey saddle surface. For more information about hyperbolic and cyclic equations visit the previous post.

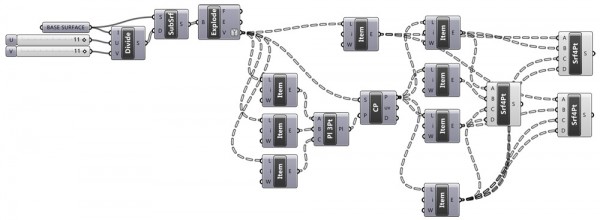[1]

As always, please save your work before testing such things. In some cases, this definition might exhaust your CPU depending on the surface and parameters you assigned.

Source URL: https://www.designcoding.net/quadrilateral-surface-tesselation/

---