Puzzling

by Tuğrul Yazar | March 21, 2012 01:47

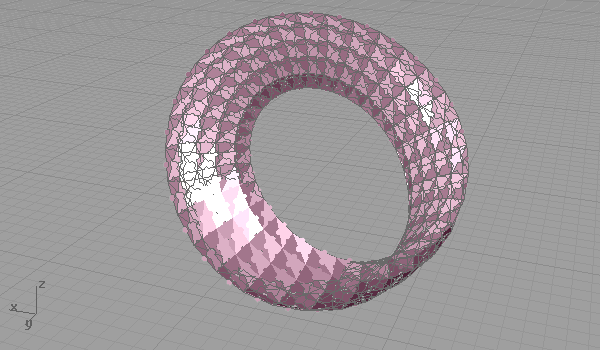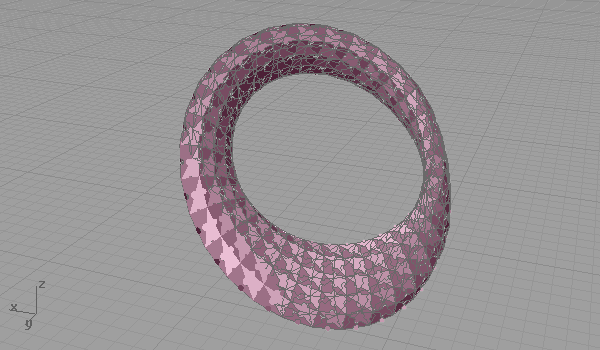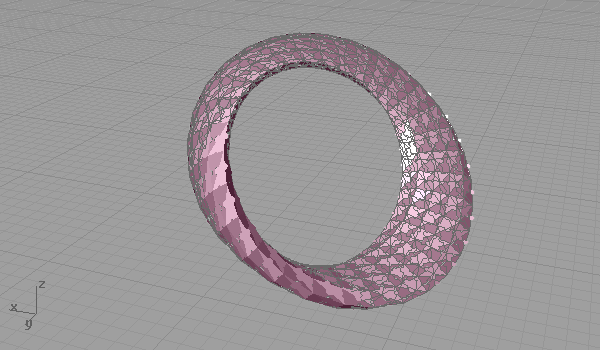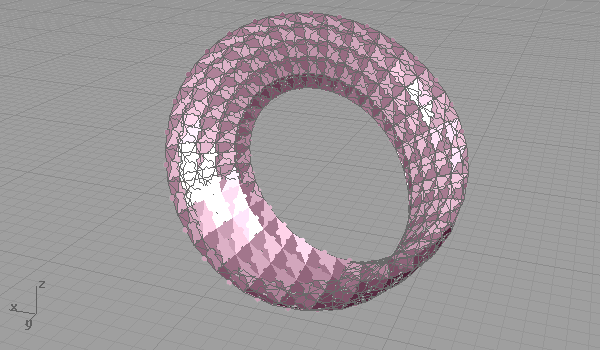
Nowadays, I found myself back into traditional hand sketching. Several failed attempts on Grasshopper led me back there. NURBS (and Grasshopper) somehow limits our conception of surfaces to four-cornered (or two-directional) manifolds. Although it sounds like limiting our designs, having four-cornered component spaces has still lots of experimental fields for designers. Escher is a cult person, who transforms the euclidean coordinate system to meet his design intentions. There are lots of interesting research about him, and he shows us how it’s possible to manipulate some fundamental geometric systems, although we believe that they are eternal. While I was planning to simulate Escher’s famous tessellations for real-time sketching, this exercise led me to the puzzle surfaces.

[1]

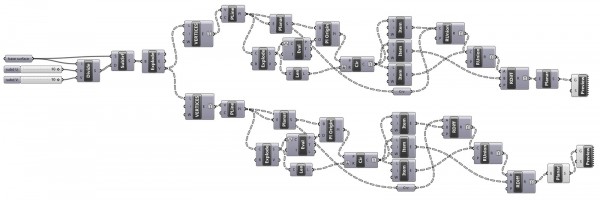
Grasshopper definition (found here: [GHX: 0.8.0066][2]) needs serious optimization, but it immediately shows how it becomes easy for Grasshopper if the target surfaces are four-cornered (or triangulated). This definition creates regions by adding and subtracting circular planes from the surface’s triangular subsets. It clearly opens the way to more complex tessellations and some other fabrication issues like deciding the size and side of each puzzle connection, and preparing the output for laser cutting (for example, cutting along each triangular face, and scoring the connections so that we may fold them to match the neighboring face). That was a nice evening study, puzzling me a lot, yet much more could be done.

Source URL: https://www.designcoding.net/puzzling/

---