Poincaré’s Hyperbolic Disk

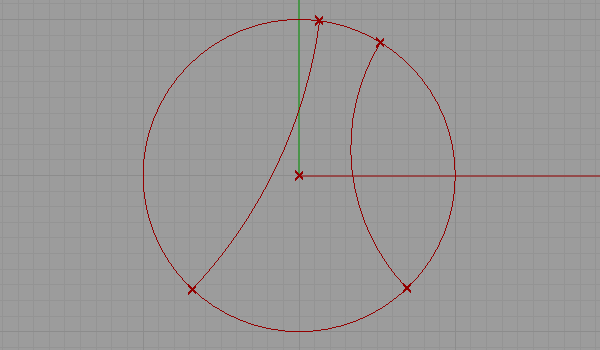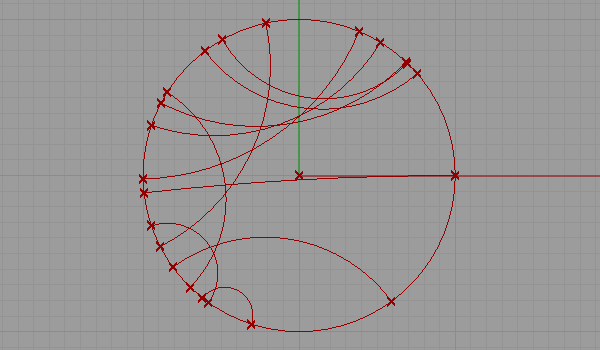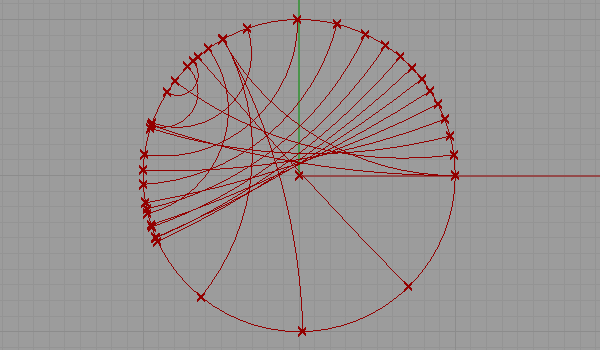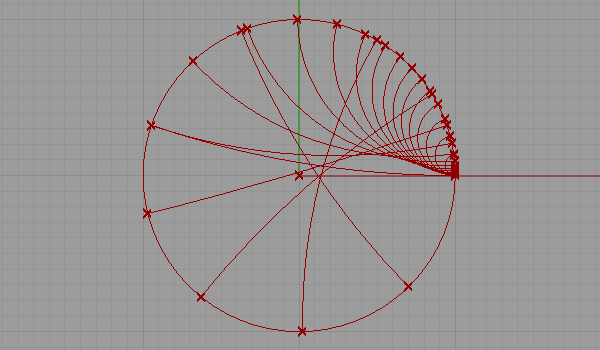
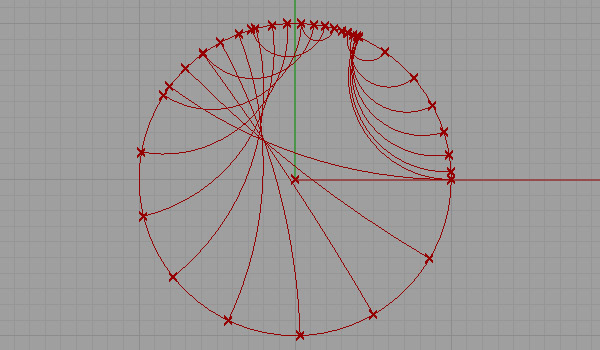
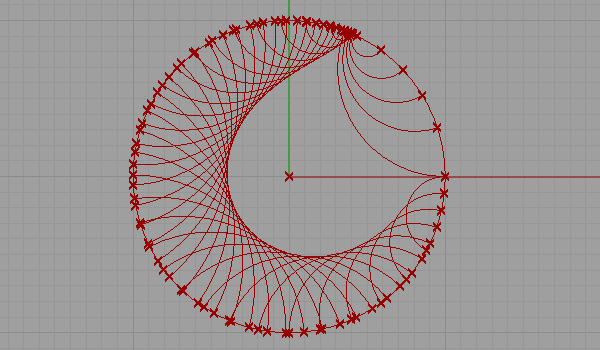
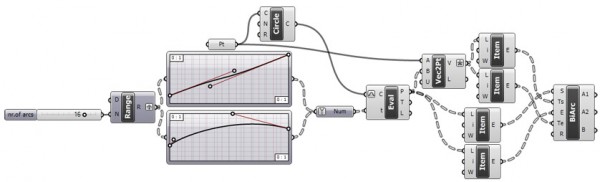
This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made arc component of Grasshopper3d, showing start and end points along with start and end tangent vectors pointing at the center of the disk. The initial tests were very funny and interesting, but I expect much more from this representation. I’ll continue drawing regular and irregular tessellations both in 2D and 3D in this space. Here is the first attempt at the Grasshopper definition [GHX: 0.8.0066].

Here is a part of Charles Jenck’s old and famous text about non-Euclidean geometry and architecture;

The most profound question is: Why does it matter? Is the new Nonlinear Architecture somehow superior, closer to nature and our understanding of the cosmos, than Old Modernism? Is it more sensuous, functional, liveable? Is it closer to aesthetic codes which are built into perception? Has it supplanted the traditions from which it has grown – Post-Modern and Deconstructivist architecture? The answer to these questions, which implicitly justify a change, might be ‘yes’, but it is too early to tell. There are other supporting arguments of a cultural and spiritual nature: architecture, to be true to the spirit of contemporary life and the life of forms in art, must explore new languages.

Jencks, C., (1997), “Nonlinear Architecture, New Science = New Architecture?”, Architectural Design 129/7.