Penrose Tiling Generator

by Tuğrul Yazar | April 16, 2024 10:37

A Penrose tiling exemplifies a type of tiling known as aperiodic. In this context, tiling involves covering a plane with non-overlapping polygons or shapes. Aperiodic means the tiling lacks arbitrarily large repeating sections. These tilings derive their name from mathematician and physicist Roger Penrose[1], who extensively studied them during the 1970s. Despite their absence of translational symmetry, Penrose tilings can exhibit both reflection symmetry and fivefold rotational symmetry. I created a simple Penrose Tiling Generator in Grasshopper[2]. I used the subdivision rules to realize this. The definition runs a loop so the Hoopsnake add-on is necessary. The triangular mapping component of Grasshopper is the key point of this generator.

This Grasshopper definition generates Penrose tilings based on the initial tiles. It utilizes the subdivision methodology of four triangular units. Therefore, the results are based on the initial unit(s). Also, you can control the number of iterations the generator will execute. The results are filled with surfaces and colorized. The outputs of the definition are closed polylines. They represent the triangular pieces and their colorings show the Penrose tiles. To be able to use this definition you should have Hoopsnake add-on installed. Because the definition uses a loop which is not readily available in Grasshopper. I added the tiles as a separate Rhinoceros model file.

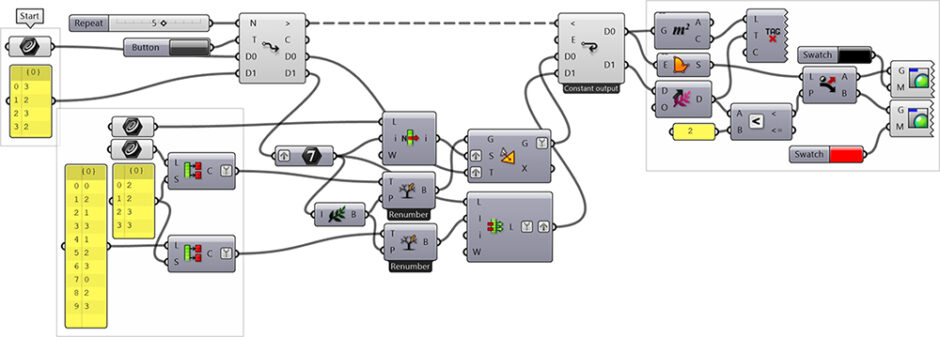
You can rebuild the definition by looking at the image above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[3] including the working Grasshopper files for the Penrose Tiling Generator and more.

Source URL: https://www.designcoding.net/penrose-tiling-generator/

---