Parquet Deformation of Islamic Patterns
by Tuğrul Yazar | February 3, 2012 02:05
This is another starting point for pattern generation study in a dataflow environment. I tried to implement the parquet deformation[1] of Islamic patterns[2] in Grasshopper[3]. I studied Hankin’s method of Islamic Pattern generation. Then I tried to simulate his process beginning with basic regular tiling (regular hexagonal tessellation). Craig S. Kaplan (here[4]) explains this and other methods in his dissertation.
A Simple Foundation
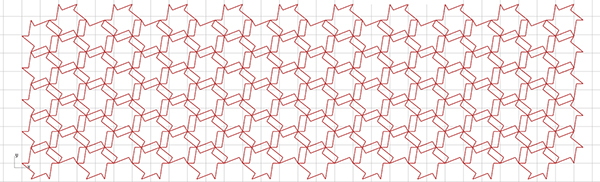
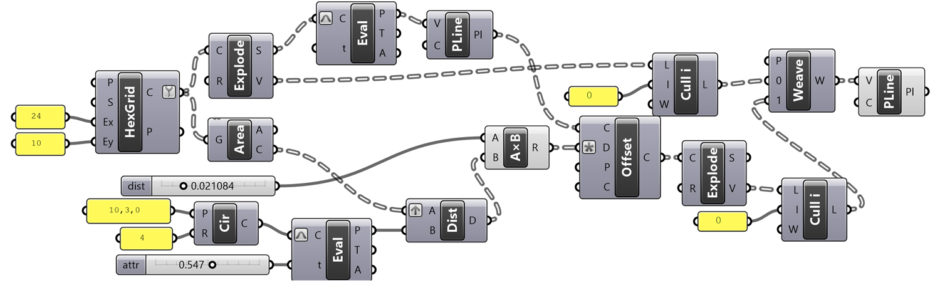
We have already experienced the result of exploding any hexagonal grid, shifting its points with the help of Evaluate Curve (Eval), and redrawing this state of hexagons with Polyline (PLine). In this application, as always, we find it useful to examine the steps of the design, the resulting geometric objects, and data structures by opening and closing the Previews of the components one by one and connecting the Panels. In the offset component, we use the negative D value to offset inward each of the shifted hexagons drawn in the previous Polyline (PLine) step.
 [5]
[5]The curves drawn in this application started with the same grid component. So their directions will always be the same. This means that there is no uncertainty that we will need the flip operation. Then, we explode our shifted and inwardly shifted hexagons with Explode. After that, we obtain the points of each hexagon from the V output. At this point, a critical process is to delete an extra point produced by Explode. We use Cull Index (Cull i) before using the Weave component.
Weaving it
When Grasshopper explodes closed curves, it produces two points overlapping. Because it creates the start and end points separately. You can also see this status by connecting a Panel. Although this process does not make any difference in terms of the image produced by this application, the fact that there are extra invisible corners in the resulting polyline curves will cause other problems in the later stages of the application. After I cleaned the points, I distributed them one by one in order and transformed them into a new point list. If you remember the Weave component, it does just that. It sorts the data lists (preferably having the same tree structure) from the two entries named 0 and 1 using the pattern in the P input.
As a result, a new list is created by removing the points from inside and outside to obtain a star-like zigzag. This zigzag structure becomes even more evident when the points in this list are redrawn with a Polyline (PLine) component in the last step. You can observe different patterns by playing with Number Sliders.
Parquet Deformation of Islamic Patterns
This method, which is a simplified version of the drawing method developed by Ernest Hankin about the patterns in Islamic art in the 1930s, is transformed into a pattern deformation with the participation of the attractor point. The whole operation is the same as in the previous application. But instead of using a fixed Offset value for each cell, I linked this value to the distances of the centers of the hexagons from a moving point. The impact point makes a rotation on a circle. The * sign you see in the D output of the Offset component used in this application is an expression. In the example, by entering the -x expression here, I converted the incoming numbers to negative.
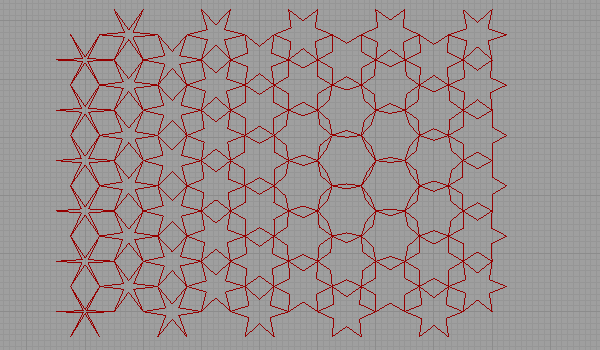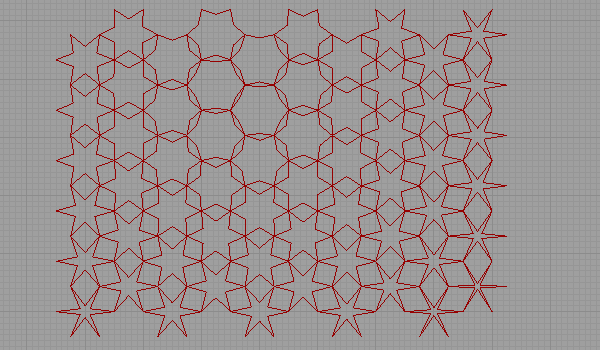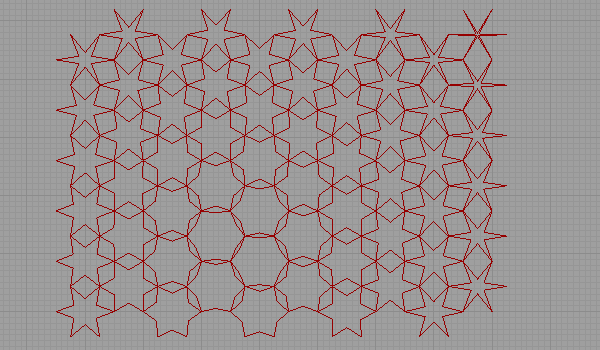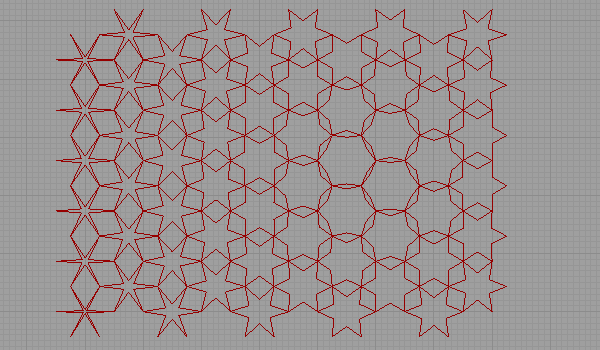
This approach is especially good at deformations from various attractors (without breaking the visual continuity). Further research should include other generation methods. For example, the rule-based approach that, at first sight, seems to fit a computer simulation better. But first, I have to solve the semi-regular tilings as they don’t exist as ready-made components yet.

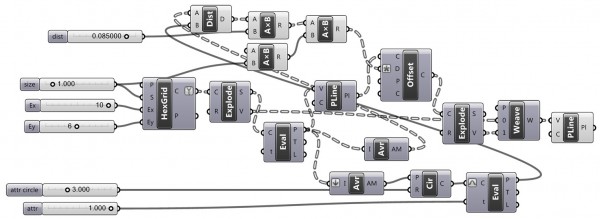
Update: I’ve optimized the definition. Here is a better version:
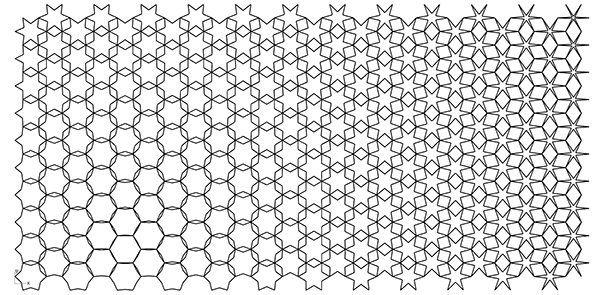
 [6]
[6]You can rebuild the definition by looking at the two definitions above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[7] including the working Grasshopper files for the Parquet Deformation of Islamic Patterns and more.
- parquet deformation: https://www.designcoding.net/category/research/pattern-deformations/
- Islamic patterns: https://www.designcoding.net/category/research/islamic-patterns/
- Grasshopper: https://www.designcoding.net/category/tools-and-languages/grasshopper/
- here: https://cs.uwaterloo.ca/~csk/other/phd/
- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2023/06/2012_02_03-starpre-def.jpg
- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2023/06/2012_02_03-star1-def.jpg
- Here is the link to my Patreon page: https://www.patreon.com/posts/parquet-of-85367012?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
Source URL: https://www.designcoding.net/parquet-deformation-of-islamic-patterns/