Parametric point on a Bezier curve

by Tuğrul Yazar | February 1, 2024 23:10

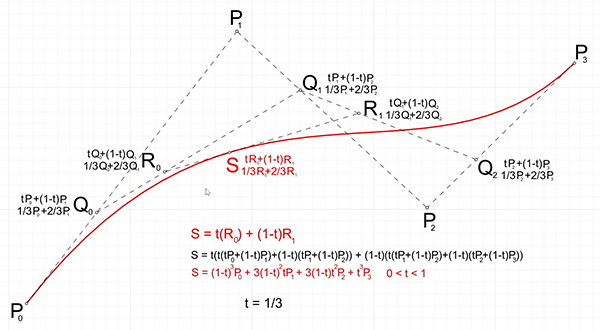
In this short tutorial, I am going to show you how to locate a parametric point on a Bezier[1] curve. This will be a third-degree cubic Bezier[2] curve. So, I start by placing four control points. I name these points from P0 to P3. Then, I connect them by a polyline in order. I explode the polyline into the segments. The parameter of my point must be a number between 0 and 1. I will divide the segments, so I chose a fractional number of 1/3. Then, I divide each segment into 3 and pick and label the points at one-third. I continue the same process with the new points. Connect them with a polyline, explode, and divide each segment into three, and pick and label the first one-third.

Again, new points are connected with a single line segment. At this stage, the algorithm is finished since we are left with one single point labeled as S. Now, I draw a degree three curve in Rhino by using the initial control points. You see that the last point I located is on the b-spline curve. The point S represents the point on this curve at t = 1/3. You can change the t value and re-calculate this to locate any point on the curve. You can combine all of the linear interpolations into one single mathematical expression to develop a general formula for third-degree Bezier curves. Now, you can locate any parametric point on a Bezier curve by either drawing or calculating.

Source URL: https://www.designcoding.net/parametric-point-on-a-bezier-curve/

---