Parametric Pendentives

by Tuğrul Yazar | August 1, 2024 17:51

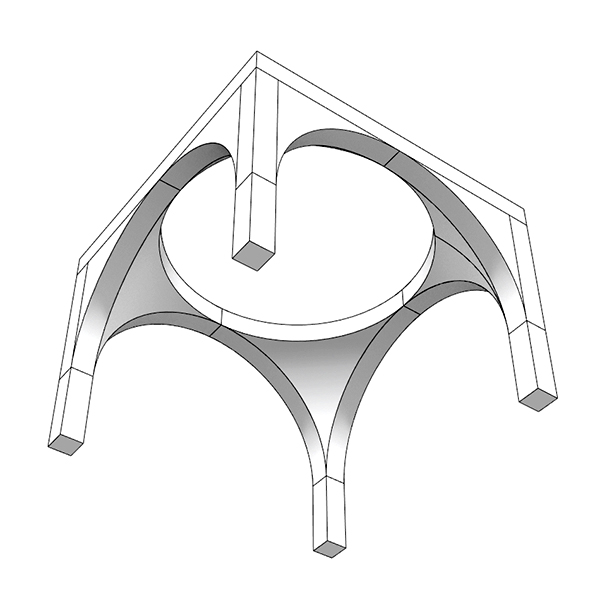
A pendentive is an architectural feature used in domed structures. It is a triangular section of a sphere that allows for the transition from a square or polygonal base to a circular or polygonal dome. Pendentives curve upward from the corners of the base and support the dome above. They help distribute the dome’s weight more evenly and enable the construction of a dome over a non-circular base. I created this Grasshopper model using a technique I had previously presented here[1]. The Parametric Pendentives definition includes the conventional square, hexagon, and octagon bases. Also, I included other interesting ones such as triangular, heptagonal, etc. Since it is geometrically stable, you can increase the number of sides. The formula for the height of the arches is R x sin(pi/n) where n is the number of sides and R is the radius of the dome.

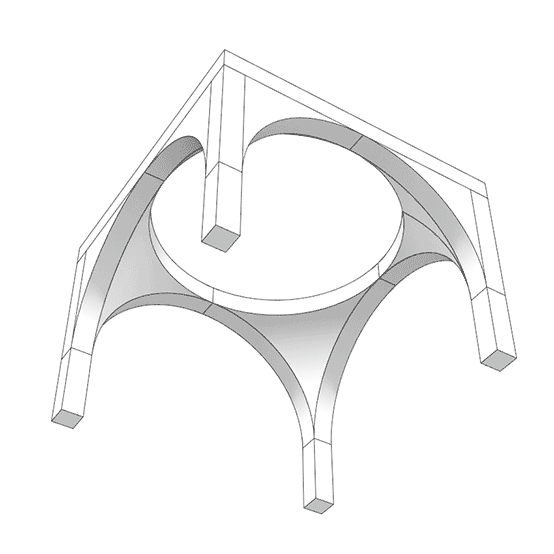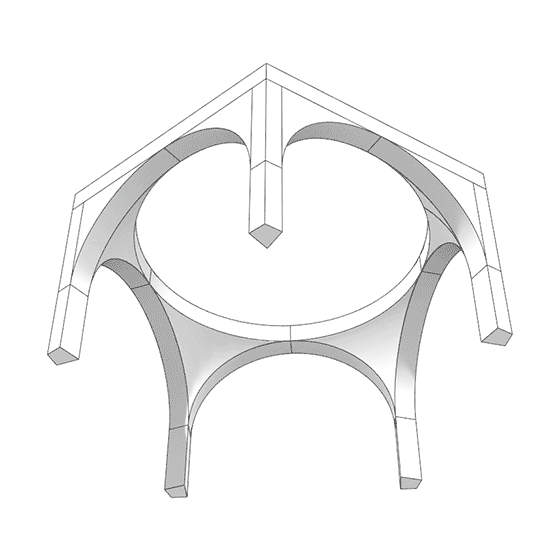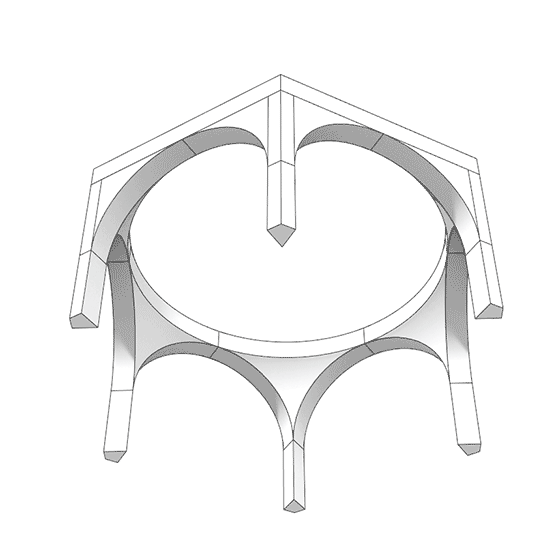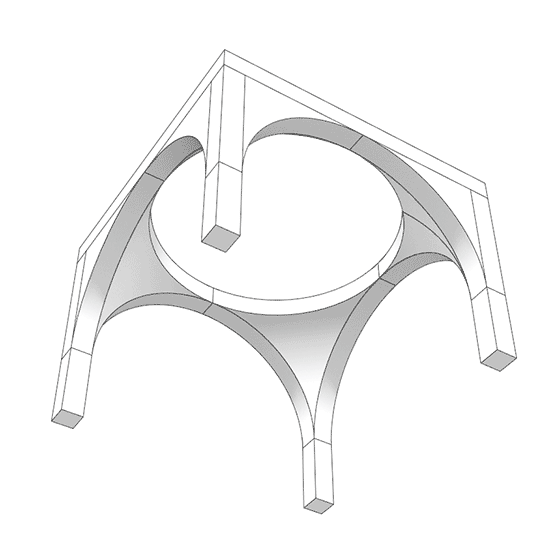
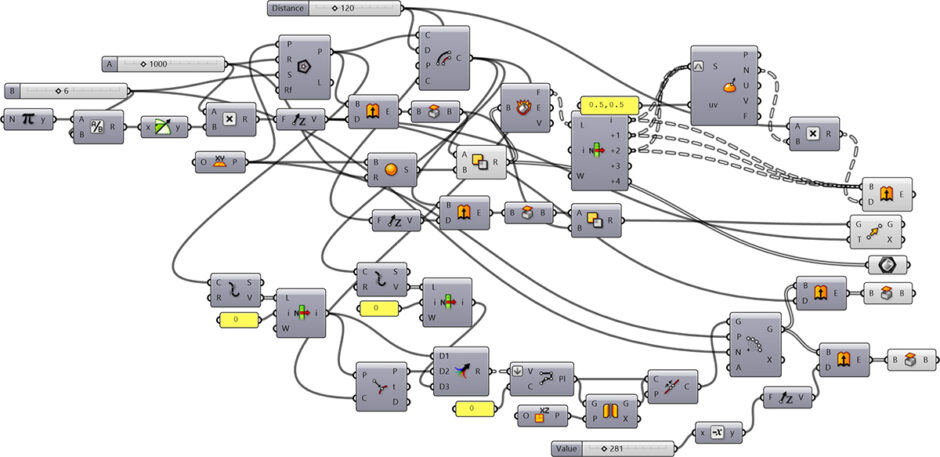
This Grasshopper definition generates parametric structures with polygonal bases and pendentives. I created the parametric model in Grasshopper with native components. So, no add-ons are necessary for it to work. The inputs are the number of sides, the spanning distance, and the height of the columns. The parametric model does not include the dome geometry. The output of the model is a set of closed solid objects. Therefore, the outputs are ready for 3d printing. Also, you can use this model for educational purposes.

[2]

You can rebuild the definition by looking at the diagram above. The model is a pure geometric construction without any Rhino input. However, if you want to support my website by downloading my working Grasshopper file, would you like to be one of my Patreons? The link to my Patreon page[3] includes the Grasshopper file for the Parametric Pendentives and more. Thank you. 

Source URL: https://www.designcoding.net/parametric-pendentives/

---