I have created a straightforward Grasshopper code that generates a Voronoi diagram on a surface. Then, it adds thickness to form a structure called a “Voronoi Cage.” In the initial step, I project a surface onto the ground plane (Z=0). The projected frame serves as the boundary for two operations: generating random points using the Populate 2D (Pop2D) function and calculating the Voronoi diagram based on these points. The resulting […]

I studied the interlocking joint details in Grasshopper here and here. This time, the interlocking structures were revisited with a cleaner code and an in-depth explanation. I believe that this is a very good educational exercise for learning the potential of the native Grasshopper components. The Preparations The Region Difference (RDiff) component is used to create the interlocking detail of a surface that is contoured with bi-directional spacing. In the […]

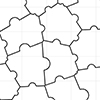
In this Voronoi puzzle exercise, we derive two-dimensional puzzles by using Voronoi diagrams. This is similar to my previous studies here, and here. Part 1: The Random Voronoi Diagram In section 1 of the below image, I use a rectangular region to generate random points. Then, I create a standard Voronoi diagram by using those points. Finally, I explode the Voronoi cells. Part 2: The Voronoi Puzzle Details In the […]

Let’s continue the Grasshopper for Beginners series. We start with the traditional “Hello World!” displayed on the Rhino screen: Placing the Components In most CAD programs, the text creation function, which is the equivalent of the Text command, is performed by a component called Text Tag (Tag) in GH. The Text Tag (Tag) component is in the Dimension panel under the Display tab. If you’re not comfortable with tabs and […]

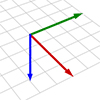
In the Digital Fabrication course, I needed to explain the plane orientation and rotation angles. This is why I prepared this Spatial Recognition Test. This is an important topic regarding the matching of the TCP (tool center point) plane of the robot and the plane(s) designers generate. In Rhino, we define a construction plane by red (X), green (Y), and blue (Z) colors. The relative positions among those axes are […]

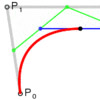
Below is the Python code you can run in Rhino, that draws a cubic Bézier curve (degree 3). As you can see, the Rhino Python code is very slow and inefficient because we calculate every point with lots of computations. Instead, we can use the spline formulae to make this quicker but I wanted to show that the mathematical construction is parallel to the geometric one. This is a nested […]

We will see a simple Rhino Python exercise here. I called these Polygon Fractals (or Pentaflakes sometimes). It is both educational and fun to play with them. In Rhino, it can be a good exercise for basic CAD commands and transformations such as move, copy, and scale, and precision drawing operations such as object snapping. Also, in Grasshopper, it can be a good challenge for looping. In Rhino Python, it […]

This is a classical method of generating tree-like forms utilizing a simple command “Arc SED”. The idea is simple, as the command draws arcs using an input direction vector, so this could easily be implemented creating a “smooth” composition of curves just by iteration. Actually, this has been a previous study, discussed before here, using Hoopsnake. Now, this time I’m implementing the same algorithm using Anemone and a couple of other […]

Finally, I had a chance to test and understand the force fields tab in Grasshopper. It creates a continuous vector field inside of a given boundary. Therefore, it is very useful if you want to create an effect of the continuous presence of a force, such as gravity. The Wikipedia definition of a vector field is very basic and understandable: In vector calculus and physics, a vector field is an assignment of a vector to each point […]

While testing Anemone components for Grasshopper, I accidentally generated these branches by looping. In fact, I was trying to develop the definition that mimics the well-known “Arch SED” component method. This method uses the tangent vectors for the endpoints of the arcs. Then, it iterates the process in a random fashion so that the branches (arcs) join nicely. Anyway, this definition develops new branches from a previous one. It does […]

Here is a test of the optical flow component of Firefly. You can check the Firefly add-on to Grasshopper here. As an ongoing research project, I’ve been searching for a suitable platform to study responsive geometric patterns. This initial study focuses on one particular effect of Firefly, the optical flow that outputs the direction vectors on a given webcam input. I developed traces of it by joining endpoints of these […]

Force fields might be one of the most influential component sets of Grasshopper. Thus it also becomes a de-facto standard design approach like the Voronoi subdivision. There are beautiful examples of this mathematical solution. Here is a good explanation of mathematics underneath, and here are my previous studies. I tried to use the Grasshopper’s force field components and see how it looks like when animated. Thus, multiple spin forces are merged […]

Instead of searching for an iterated and rule-based variety, this method captures instances of spatial deformation by transforming the hyperframe. This liberates us from a classical understanding of pattern deformations that are enframed within regular polygons, mostly rectangles or hexagons. Grasshopper has a built-in component to study such variety. The spatial Deform component gets vectors as inputs and transforms any given geometric object according to it. This website has also […]

I’ve seen beautiful examples of similar compositions made using vector field components in Grasshopper. I just tried to make my own animate field lines to see how they float over force dynamics. In essence, these compositions could also be done using regular vector components but the field components make life much easier by merging different forces together rather quickly. Here is my Grasshopper definition (be careful it may slow the […]

This is another final project of the three-day workshop at YTU, named Infections. A conceptual framework is developed by Bahar Aybudak (METU) and Zeynep Gür (ITU). The cellular forms come together to set the existing wall (host body). The wall represents the body structure, in which in case of any infection, various challenges could be seen in parallel with the immune system. The struggle with the mentioned infection is observed through […]

After playing with vector fields in 2d (here) it was quite easy to create a 3d surface deformation. Here is my first experiment on a regular triangular grid’s three-dimensional behavior within a vector space, that includes a point charge of varying z coordinates. That makes field lines escape to a bounding box, instead of a bounding rectangle. Again, you may play with force decay, the number of samples, and the […]

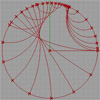
This is my first attempt at representing a non-euclidean space. There are several representations of a non-euclidean space in euclidean means such as Beltrami-Klein or Klein, Poincare, Poincare half-plane, and Weierstrass. Here, I tried to understand Poincare’s approach. Random straight lines are drawn on a hypothetical hyperbolic space using a simulation of Poincare’s famous disk representation. Although there is a precise description of the disk and its construction, I used a ready-made […]