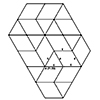
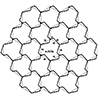
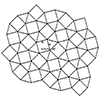
Stellation of polyhedra refers to the process of extending the faces (or edges) of a polyhedron outward to form new, more complex shapes. These new shapes, called stellations, are created by adding extra vertices, edges, and faces that “project” outward from the original polyhedron’s structure. You can create an infinite number of new polyhedral forms, depending on how you extend the faces and edges. In this short tutorial video, I […]

A dual polyhedron is a concept in geometry where two polyhedra are related in such a way that the vertices of one polyhedron correspond to the faces of the other, and the faces of the first polyhedron correspond to the vertices of the second. The process of creating a dual polyhedron is called duality, and it applies to many regular, semi-regular, and some irregular polyhedra. In the case of Platonic […]

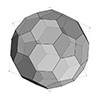
The truncated octahedron is an Archimedean solid, characterized by a mix of hexagonal and square faces, and it has a very symmetrical and regular structure. Buckminster Fuller called this solid “Mecon”. The truncation process includes the cutting the edges of a polyhedron. We do this by dividing every edge of the polyhedron into 1/3s. Then, we carefully re-connect these division points to generate new, planar polygons. In the case of […]

Buckminster Fuller used the term “dymaxion” for a variety of his designs, and one of these was the dymaxion map. It was based on the geometry of a polyhedron. While the dymaxion map is more directly related to the icosahedron, Fuller’s work often involved using other polyhedral shapes. One of them is the cuboctahedron. He used this term for various conceptual and practical designs, particularly in the context of his […]

A Buckyball, (or Fullerene), is a molecule of 60 carbon atoms with a structure resembling a soccer ball. It is a specific type of fullerene, often referred to as C60, where the carbon atoms form a series of pentagons and hexagons in a pattern that creates a spherical shape. This structure is similar to the arrangement found in a truncated icosahedron, with 12 pentagonal and 20 hexagonal faces. The buckyball […]

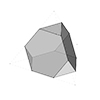
Truncation in mathematics and geometry refers to cutting off parts of a shape, typically the vertices, edges, or other extremities, to create a new modified figure. This process is often used with polygons, polyhedra, or functions. A truncated tetrahedron is a polyhedron we can derive from a regular tetrahedron by truncating (cutting off) its four vertices. This process creates a new shape with additional faces while maintaining its symmetry. In […]

In Rhino, layouts are used to prepare drawings for printing or presentation. They provide a way to organize and display 2D views of your 3D model, such as top, front, side, and perspective views, in a way suitable for producing printed or published documents. In this short tutorial video, I show the basic usage of the Rhinoceros layout system. So, this Rhinoceros Layout Tutorial video is for beginner-level CAD users. […]

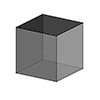
A cube is a three-dimensional shape with six square faces, twelve edges, and eight vertices. It is one of the most familiar geometric solids and is a special type of rectangular prism where all sides are of equal length. A cube has a high degree of symmetry. Angles between its faces are right angles. It is often referred to as a “regular hexahedron”. Also cube is one of the Platonic […]

A dodecahedron is a three-dimensional polyhedron with twelve flat, regular pentagonal faces, twenty vertices, and thirty edges. It is one of the Platonic solids and is highly symmetrical, with each face being a regular pentagon. The dodecahedron’s shape is unique among the Platonic solids because its faces are polygons with five sides, unlike the others which have triangular faces. Due to its symmetry, the dodecahedron has been used in various […]

An icosahedron is a three-dimensional polyhedron with twenty triangular faces, twelve vertices, and thirty edges. It is one of the five Platonic solids and is highly symmetrical, with all faces being equilateral triangles. A regular icosahedron has equal edge lengths and angles between its faces, making it one of the most symmetrical shapes in three-dimensional space. In this short tutorial video, I am modeling and unrolling an icosahedron. I studied […]

An octahedron is a three-dimensional polyhedron with eight triangular faces, six vertices, and twelve edges. It is one of the Platonic solids and has high symmetry, with all of its faces being equilateral triangles. A regular octahedron can be visualized as two pyramids joined at their bases. It has the same number of faces as a cube has vertices, and the same number of vertices as a cube has faces. […]

A tetrahedron is a three-dimensional shape with four triangular faces, four vertices, and six edges. It is the simplest polyhedron and, in its regular form, has equilateral triangles as faces, with all edges of equal length. Thus, known as one of the Platonic solids, a regular tetrahedron is highly symmetrical, and its shape is considered stable and efficient in many natural and man-made structures. In this short tutorial video, I […]

Lattice deformation in parametric design refers to the process of manipulating a grid or mesh structure so that it changes shape in response to specific inputs or parameters. We use this approach widely in computational design for creating complex, organic forms and adaptive systems. Also, lattice deformation can be applied in architectural facades, structural systems, and product design where adaptability and aesthetic fluidity are desired. In this short tutorial video, […]

Parquet deformation refers to a transformation technique applied to a grid or tiling pattern, particularly one that resembles traditional parquet flooring, to create visually interesting and dynamic patterns. This concept is used in parametric design to alter repeating geometric tiles, producing effects such as warping, bending, or otherwise deforming the original pattern while maintaining an overall cohesive layout. In this short tutorial video, I am explaining the drawing of Crosswise […]

Using a compass and straightedge enables precise geometric constructions, allowing for the creation of complex tessellations. To begin these constructions, a single starting point is sufficient. Circles, which represent a collection of points at a specific distance from the center, and straight lines, which represent a collection of points in a particular direction, are utilized for geometric constructions. In this short tutorial, we move on with the beginner-level drawing exercises. […]

Escher tilings, inspired by the work of Dutch artist M.C. Escher, are inspiring tessellations that cover a plane using repeated geometric shapes without gaps or overlaps. He often used interlocking, recognizable figures like animals and birds to create these patterns, blending art with mathematical precision. His tilings explore symmetry, transformations, and the interplay between two- and three-dimensional space. Escher’s work has influenced both artistic and mathematical fields, particularly in the […]

Snub Square Tiling is a semi-regular tessellation of the plane, composed of two squares and three regular triangles at each vertex. The arrangement of these two regular shapes seamlessly covers the plane without any gaps or overlaps. It is one of the eight semi-regular tessellations known in geometry. The dual of Snub Square Tiling is Cairo Pentagonal Tiling, which we will explore later. In this short tutorial, I am drawing […]