More Vector Operations in Rhino Python
This is the continuation of my new project of re-creating the parametric curve and surface methods of Rhino via Python scripting. If you remember, I started with the building block of vector operations, here and here. Then, I defined vector addition and multiplication, before going deeper into the geometric calculations. In fact, they are using the previously defined addition and multiplication methods.
New Vector Operations: Subtraction and Reversing
In the future, we are going to need to reverse a vector, which means changing its direction without changing the orientation. Therefore, this can be easily done by multiplying the vector with -1. Secondly, we are going to subtract one vector from the other. This looks rather complicated if you think about it. However, since we know how to reverse a vector, it is possible to say that, subtracting a vector from another one is just reversing one vector and then adding it to the other one. Because, a-b = a+(-b).
import rhinoscriptsyntax as rs
class Vector:
def __init__(self, point):
self.components = point
def display(self, origin=[0,0,0]):
v = self.components
tip = [v[0]+origin[0], v[1]+origin[1], v[2]+origin[2]]
line = rs.AddLine(origin, tip)
rs.CurveArrows(line, 2)
def add(vA, vB):
v1 = vA.components
v2 = vB.components
addition = [v1[0]+v2[0], v1[1]+v2[1], v1[2]+v2[2]]
return Vector(addition)
def multiply(self, s):
v = self.components
return Vector([v[0]*s, v[1]*s, v[2]*s])
def reverse(self):
return self.multiply(-1)
def subtract(vA, vB):
return Vector.add(vA, vB.reverse())Line-by-line Explanation
Below is a more formal, line-by-line explanation, if you need it:
| Line | Explanation |
| 1-17 | Already explained here. |
| 18 | Define a new method called “reverse”. |
| 19 | Return the value of multiplication by -1. So, this will call the multiply method with the scalar value of -1 as the input. If you remember the previous day, the multiplication method multiplies the number with the three coordinates separately and returns a new vector object. Thus, this vector object is caught by the reverse method and then, returned to the user. It is like playing volleyball with objects. |
| 20 | Define a new method called “subtract” by taking two inputs. Notice that this method does not take “self” as an input. This means this method is a general method for the whole class, not for single objects (we refer to “self”). |
| 21 | As explained above, we use the addition of two vectors, by reversing one of them to achieve subtraction. Because, a-b = a+(-b). |
Testing the New Vector Operations
The below code will call the reverse method and display its result in the Rhino viewport. Note that you should add the below code to the above one otherwise it won’t work.
myvector1 = Vector([3,5,0])
myvector2 = myvector1.reverse()
myvector1.display()
myvector2.display()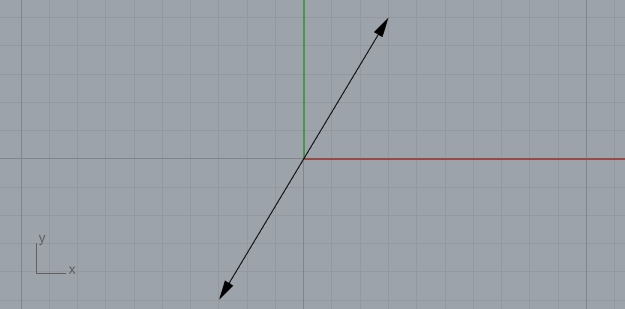
Below, we use the second method. Notice that the usage of the class method is different. If you remember, the subtraction method was a class method, which does not take “self” as an input. This is why we are using that method not by calling it from a specific object (like myvector1) but from the name of the whole class (Vector).
myvector1 = Vector([3,5,0])
myvector2 = Vector([8,2,0])
myvector3 = Vector.subtract(myvector1, myvector2)
myvector1.display()
myvector2.display()
myvector3.display()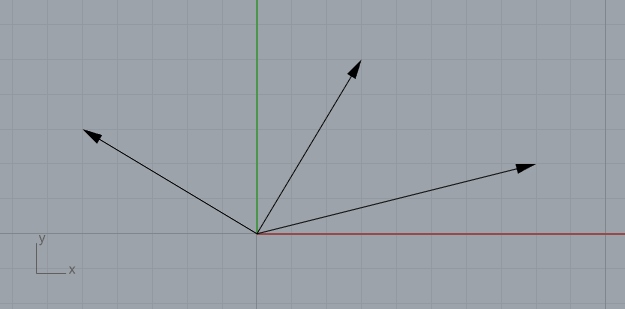
I know, this was a simple step, a little too simple maybe. Thus, tomorrow, we are going to make a bigger step, adding more vector operations, to measure the magnitudes (length) of vectors, and “normalize” them.








